Parabola 1 Question 14
14. Let
(2012)
Show Answer
Solution:
- PLAN Parametric coordinates for
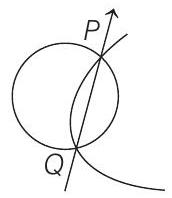
Description of Situation As the circle intersects the parabola at
Thus, area of






