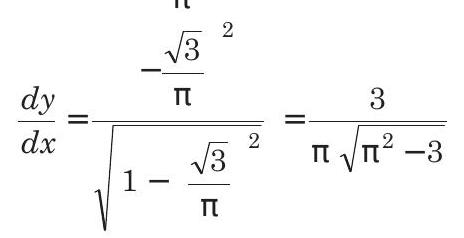Limit Continuity and Differentiability 7 Question 29
29. Let $a, b \in R$ and $f: R \rightarrow R$ be defined by $f(x)=a \cos \left(\left|x^{3}-x\right|\right)+b|x| \sin \left(\left|x^{3}+x\right|\right)$. Then, $f$ is
(2016 Adv.)
(a) differentiable at $x=0$, if $a=0$ and $b=1$
(b) differentiable at $x=1$, if $a=1$ and $b=0$
(c) not differentiable at $x=0$, if $a=1$ and $b=0$
(d) not differentiable at $x=1$, if $a=1$ and $b=1$
Show Answer
Answer:
Correct Answer: 29. (A) $\rightarrow$ p, q, r, s; (B) $\rightarrow p, s$; (C) $\rightarrow r, s$; (D) $\rightarrow p, s$
Solution:
- Here, $(\sin y)^{\sin \frac{\pi}{2} x}+\frac{\sqrt{3}}{2} \sec ^{-1}(2 x)+2^{x} \tan {\log (x+2)}=0$
On differentiating both sides, we get
$$ \begin{aligned} & (\sin y)^{\sin \frac{\pi}{2} x} \cdot \log (\sin y) \cdot \cos \frac{\pi}{2} x \cdot \frac{\pi}{2} \\ & +\sin \frac{\pi}{2} x(\sin y)^{\sin \frac{\pi}{2} x-1} \cdot \cos y \cdot \frac{d y}{d x} \\ & +\frac{\sqrt{3}}{2} \cdot \frac{2}{(2|x|) \sqrt{4 x^{2}-1}}+\frac{2^{x} \cdot \sec ^{2}{\log (x+2)}}{(x+2)} \\ & \quad+2^{x} \log 2 \cdot \tan {\log (x+2)}=0 \end{aligned} $$
Putting $x=-1, y=-\frac{\sqrt{3}}{\pi}$, we get
