Inverse Circular Functions 3 Question 5
5. If $x=\sin ^{-1}(\sin 10)$ and $y=\cos ^{-1}(\cos 10)$, then $y-x$ is equal to
(2019 Main, 9 Jan II)
(a) 0
(b) 10
(c) $7 \pi$
(d) $\pi$
Show Answer
Answer:
Correct Answer: 5. (d)
Solution:
- The graph of $y=\sin ^{-1}(\sin x)$ is
$\therefore \quad x=\sin ^{-1}(\sin 10)=-10+3 \pi$
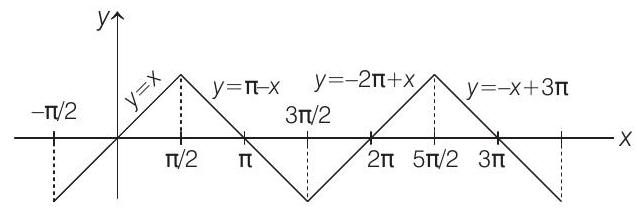
and the graph of $y=\cos ^{-1}(\cos x)$ is
$\therefore \quad y=\cos ^{-1}(\cos 10)=-10+4 \pi$
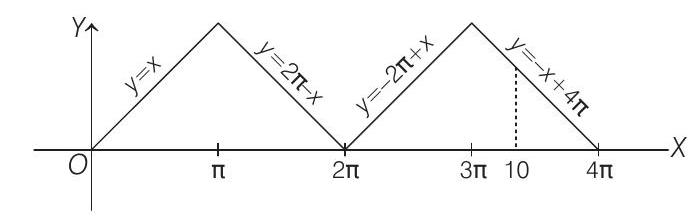
Now, from Eqs. (i) and (ii),
$ y-x=(-10+4 \pi)-(-10+3 \pi)=\pi $
