Indefinite Integration 2 Question 5
5. Given a function
Integer Answer Type Question
Show Answer
Solution:
- Let
On differentiating w.r.t.
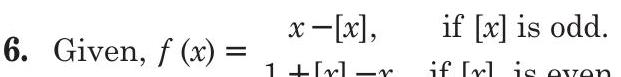
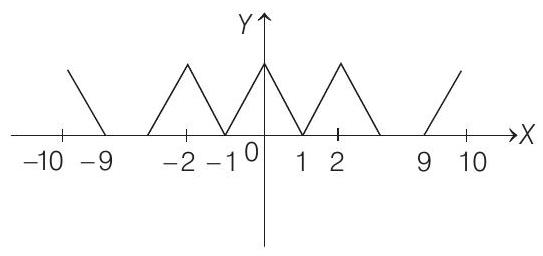
Now,
and






