Hyperbola 1 Question 9
10.
Consider a branch of the hyperbola
with vertex at the point
(a)
(b)
(c)
(d)
(2008, 3M)
Show Answer
Answer:
Correct Answer: 10. (b)
Solution:
- Given equation can be rewritten as focal chord
For point
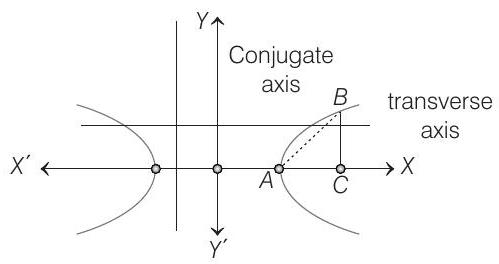
For point
Now,
and






