Ellipse 2 Question 23
23. Suppose that the foci of the ellipse $\frac{x^{2}}{9}+\frac{y^{2}}{5}=1$ are $\left(f _1, 0\right)$ and $\left(f _2, 0\right)$, where $f _1>0$ and $f _2<0$. Let $P _1$ and $P _2$ be two parabolas with a common vertex at $(0,0)$ with foci at $\left(f _1, 0\right)$ and $\left(2 f _2, 0\right)$, respectively. Let $T _1$ be a tangent to $P _1$ which passes through $\left(2 f _2, 0\right)$ and $T _2$ be a tangent to $P _2$ which passes through $\left(f _1, 0\right)$. If $m _1$ is the slope of $T _1$ and $m _2$ is the slope of $T _2$, then the value of $\frac{1}{m _1^{2}}+m _2^{2}$ is
(2015 Adv.)
Show Answer
Answer:
Correct Answer: 23. (4)
Solution:
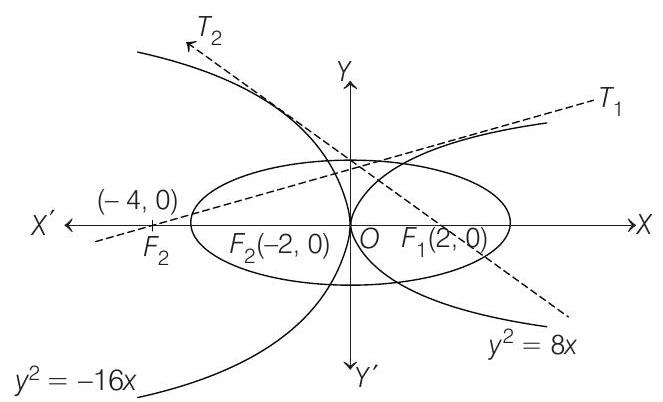
Tangent to $P _1$ passes through $\left(2 f _2, 0\right)$ i. e. $(-4,0)$.
$ \begin{aligned} & \therefore & T _1: y & =m _1 x+\frac{2}{m _1} \\ & \Rightarrow & 0 & =-4 m _1+\frac{2}{m _1} \\ \Rightarrow & & m _1^{2} & =1 / 2 \end{aligned} $
Also, tangent to $P _2$ passes through $\left(f _1, 0\right)$ i.e. $(2,0)$.
$ \begin{aligned} & \Rightarrow \quad T _2: y=m _2 x+\frac{(-4)}{m _2} \\ & \Rightarrow \quad 0=2 m _2-\frac{4}{m _2} \\ & \Rightarrow \quad m _2^{2}=2 \\ & \therefore \quad \frac{1}{m _1^{2}}+m _2^{2}=2+2=4 \end{aligned} $
