Ellipse 2 Question 13
13. Tangents are drawn to the ellipse $x^{2}+2 y^{2}=2$, then the locus of the mid-point of the intercept made by the tangents between the coordinate axes is
(2004, 1M)
(a) $\frac{1}{2 x^{2}}+\frac{1}{4 y^{2}}=1$
(b) $\frac{1}{4 x^{2}}+\frac{1}{2 y^{2}}=1$
(c) $\frac{x^{2}}{2}+\frac{y^{2}}{4}=1$
(d) $\frac{x^{2}}{4}+\frac{y^{2}}{2}=1$
Show Answer
Answer:
Correct Answer: 13. (a)
Solution:
- Let the point $P(\sqrt{2} \cos \theta, \sin \theta)$ on $\frac{x^{2}}{2}+\frac{y^{2}}{1}=1$.
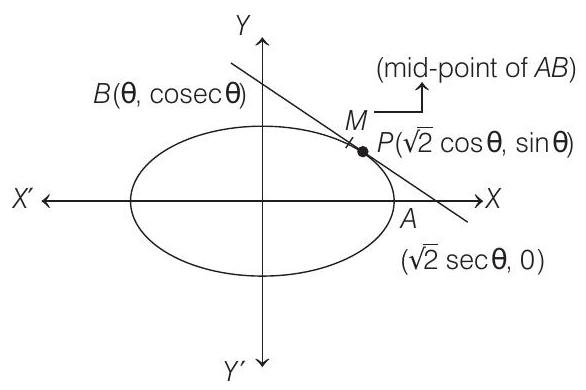
Equation of tangent is, $\frac{x \sqrt{2}}{2} \cos \theta+y \sin \theta=1$
whose intercept on coordinate axes are
$A(\sqrt{2} \sec \theta, 0)$ and $B(0, \operatorname{cosec} \theta)$
$\therefore$ Mid-point of its intercept between axes
$ \begin{aligned} \frac{\sqrt{2}}{2} \sec \theta, \frac{1}{2} \operatorname{cosec} \theta & =(h, k) \\ \Rightarrow \quad \cos \theta & =\frac{1}{\sqrt{2 h}} \text { and } \sin \theta=\frac{1}{2 k} \end{aligned} $
Thus, focus of mid-point $M$ is
$ \begin{aligned} \left(\cos ^{2} \theta+\sin ^{2} \theta\right) & =\frac{1}{2 h^{2}}+\frac{1}{4 k^{2}} \\ \Rightarrow \quad \frac{1}{2 x^{2}}+\frac{1}{4 y^{2}} & =1, \text { is required locus. } \end{aligned} $
