Ellipse 1 Question 12
13. The orthocentre of $\Delta F _1 M N$ is
(a) $-\frac{9}{10}, 0$
(b) $\frac{2}{3}, 0$
(c) $\frac{9}{10}, 0$
(d) $\frac{2}{3}, \sqrt{6}$
Show Answer
Answer:
Correct Answer: 13. $a$
Solution:
- Here, $\frac{x^{2}}{9}+\frac{y^{2}}{8}=1$
has foci $( \pm a e, 0)$
where, $ a^{2} e^{2}=a^{2}-b^{2} $
$\Rightarrow$ $ a^{2} e^{2}=9-8 $
$\Rightarrow$ $ a e= \pm 1 $
i.e. $ F _1, F _2=( \pm 1,0) $
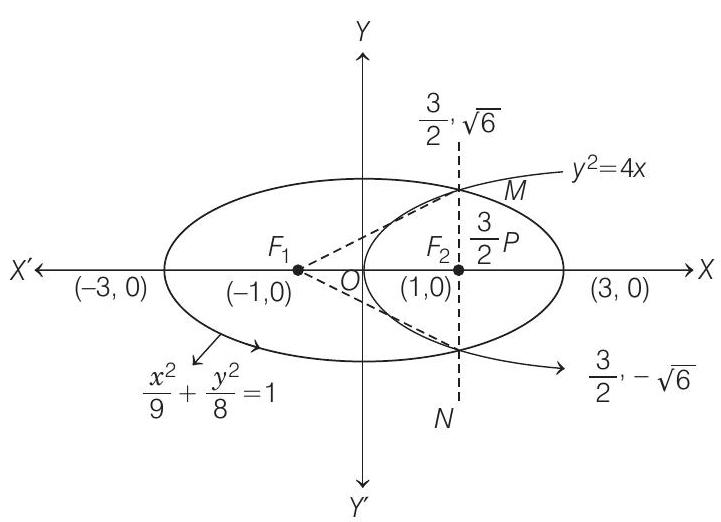
Equation of parabola having vertex $O(0,0)$ and $F _2(1,0)$ (as, $x _2>0$ )
On solving $\begin{aligned} y^{2} & =4 x \\ \frac{x^{2}}{9}+\frac{y^{2}}{8} & =1 \text { and } y^{2}=4 x \text {, we get } \\ x & =3 / 2 \text { and } y= \pm \sqrt{6}\end{aligned}$
Equation of altitude through $M$ on $N F _1$ is
$ \begin{aligned} \frac{y-\sqrt{6}}{x-3 / 2} & =\frac{5}{2 \sqrt{6}} \\ \Rightarrow \quad(y-\sqrt{6}) & =\frac{5}{2 \sqrt{6}}(x-3 / 2) \end{aligned} $
and equation of altitude through $F _1$ is $y=0$
On solving Eqs. (iii) and (iv), we get $-\frac{9}{10}, 0$ as orthocentre.
