Definite Integration Question 52
Question 52
- If $I_{n}=\int_{-\pi}^{\pi} \frac{\sin n x}{\left(1+\pi^{x}\right) \sin x} d x, n=0,1,2, \ldots$, then (a) $I_{n}=I_{n+2}$ (b) $\sum_{m=1}^{10} I_{2 m+1}=10 \pi$ (c) $\sum_{m=1}^{10} I_{2 m}=0$ (d) $I_{n}=I_{n+1}$
Numerical Value
Show Answer
Solution:
- Given
$$ I_{n}=\int_{-\pi}^{\pi} \frac{\sin n x}{\left(1+\pi^{x}\right) \sin x} d x $$
Using $\int_{a}^{b} f(x) d x=\int_{a}^{b} f(b+a-x) d x$, we get
$$ I_{n}=\int_{-\pi}^{\pi} \frac{\pi^{x} \sin n x}{\left(1+\pi^{x}\right) \sin x} d x $$
On adding Eqs. (i) and (ii), we have
$$ \begin{aligned} & 2 I_{n}=\int_{-\pi}^{\pi} \frac{\sin n x}{\sin x} d x=2 \int_{0}^{\pi \sin n x} \frac{\sin x}{\sin } d x \ & {\left[\because f(x)=\frac{\sin n x}{\sin x} \text { is an even function }\right]} \ & \Rightarrow \quad I_{n}=\int_{0}^{\pi} \frac{\sin n x}{\sin x} d x \ & \text { Now, } I_{n+2}-I_{n}=\int_{0}^{\pi} \frac{\sin (n+2) x-\sin n x}{\sin x} d x \end{aligned} $$
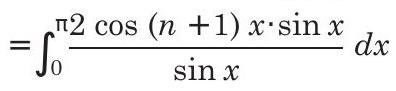
$$ \begin{aligned} & =2 \int_{0}^{\pi} \cos (n+1) x d x=2 \frac{\sin (n+1) x}{(n+1)}{ }{0}^{\pi}=0 \ & \therefore \quad I{n+2}=I_{n} \end{aligned} $$
$\Rightarrow \quad \sum_{m=1}^{10} I_{2 m+1}=10 \pi$ and $\quad \sum_{m=1}^{10} I_{2 m}=0$
$\therefore$ Correct options are (a), (b), (c).
