Definite Integration Question 29
Question 29
- If for a real number $y,[y]$ is the greatest integer less than or equal to $y$, then the value of the integral $\int_{\pi / 2}^{3 \pi / 2}[2 \sin x] d x$ is
$(1999,2 \mathrm{M})$ (a) $-\pi$ (b) 0 (c) $-\frac{\pi}{2}$ (d) $\frac{\pi}{2}$
Show Answer
Solution:
- The graph of $y=2 \sin x$ for $\pi / 2 \leq x \leq 3 \pi / 2$ is given in figure. From the graph, it is clear that
$$ [2 \sin x]=\begin{array}{ccc} 2, & \text { if } & x=\pi / 2 \ 1, & \text { if } & \pi / 2<x \leq 5 \pi / 6 \ 0, & \text { if } & 5 \pi / 6<x \leq \pi \ -1, & \text { if } & \pi<x \leq 7 \pi / 6 \ -2, & \text { if } & 7 \pi / 6<x \leq 3 \pi / 2 \end{array} $$
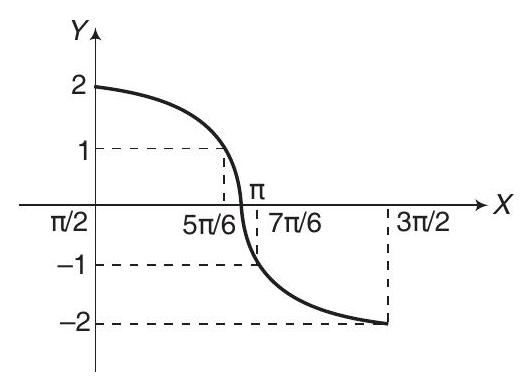
Therefore, $\quad \int_{\pi / 2}^{3 \pi / 2}[2 \sin x] d x$
$=\int_{\pi / 2}^{5 \pi / 6} d x+\int_{5 \pi / 6}^{\pi} 0 d x+\int_{\pi}^{7 \pi / 6}(-1) d x+\int_{7 \pi / 6}^{3 \pi / 2}(-2) d x$
$=[x]{\pi / 2}^{5 \pi / 6}+[-x]{\pi}^{7 \pi / 6}+[-2 x]_{7 \pi / 6}^{3 \pi / 2}$
$=\frac{5 \pi}{6}-\frac{\pi}{2}+-\frac{7 \pi}{6}+\pi+\frac{-2 \cdot 3 \pi}{2}+\frac{2 \cdot 7 \pi}{6}$
$=\pi \frac{5}{6}-\frac{1}{2}+\pi \quad 1-\frac{7}{6}+\pi \frac{7}{3}-3$
$=\pi \frac{5-3}{6}+\pi-\frac{1}{6}+\pi \frac{7-9}{3}=-\pi / 2$
