Complex Numbers 4 Question 8
8.
Let $W=\frac{\sqrt{3}+i}{2}$ and $P={W^{n}: n=1,2,3, \ldots }$.
Further $H _1=z \in C: \operatorname{Re}(z)>\frac{1}{2}$
and $H _2=z \in C: \operatorname{Re}(z)<\frac{-1}{2}$, where $C$ is the set of all complex numbers. If $z _1 \in P \cap H _1, z _2 \in P \cap H _2$ and $O$ represents the origin, then $\angle z _1 O z _2$ is equal to
(2013 JEE Adv.)
(a) $\frac{\pi}{2}$
(b) $\frac{\pi}{6}$
(c) $\frac{2 \pi}{3}$
(d) $\frac{5 \pi}{6}$
Show Answer
Answer:
Correct Answer: 8. (c, d)
Solution:
- PLAN: It is the simple representation of points on Argand plane and to find the angle between the points
Here, $P=W^{n}=(\cos \frac{\pi}{6}+i \sin \frac{\pi}{6}^{n})=\cos \frac{n \pi}{6}+i \sin \frac{n \pi}{6}$
$ H _1=z \in C: \operatorname{Re}(z)>\frac{1}{2} $
$\therefore P \cap H _1$ represents those points for which $\cos \frac{n \pi}{6}$ is + ve.
Hence, it belongs to I or IV quadrant.
$ \begin{aligned} & \Rightarrow z _1=P \cap H _1=\cos \frac{\pi}{6}+i \sin \frac{\pi}{6} \text { or } \cos \frac{11 \pi}{6}+i \sin \frac{11 \pi}{6} \\ & \therefore \quad z _1=\frac{\sqrt{3}}{2}+\frac{i}{2} \text { or } \frac{\sqrt{3}}{2}-\frac{i}{2} \end{aligned} $
Similarly, $z _2=P \cap H _2$ i.e. those points for which
$ \cos \frac{n \pi}{6}<0 $
$\therefore \quad z _2=\cos \pi+i \sin \pi, \cos \frac{5 \pi}{6}+i \sin \frac{5 \pi}{6}, \frac{\cos 7 \pi}{6}$
$+i \sin \frac{7 \pi}{6}$
$\Rightarrow \quad z _2=-1, \frac{-\sqrt{3}}{2}+\frac{i}{2}, \frac{-\sqrt{3}}{2}-\frac{i}{2}$
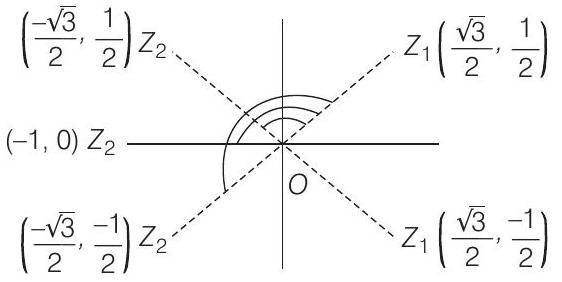
Thus, $\angle z _1 O z _2=\frac{2 \pi}{3}, \frac{5 \pi}{6}, \pi$
