SATHEE: Complex Numbers 3 Question 8

Complex Numbers 3 Question 8

8. For a non-zero complex number $z$ , let $\arg (z)$ denote the principal argument with $- π < \arg (z) \leq π$ . Then, which of the following statement(s) is (are) FALSE ? (2018 Adv.)

(a) $\arg (- 1 - i) = \frac{π}{4}$ , where $i = \sqrt{- 1}$

(b) The function $f : R \to (- π, π]$ , defined by $f (t) = \arg (- 1 + i t)$ for all $t \in R$ , is continuous at all points of $R$ , where $i = \sqrt{- 1}$ .

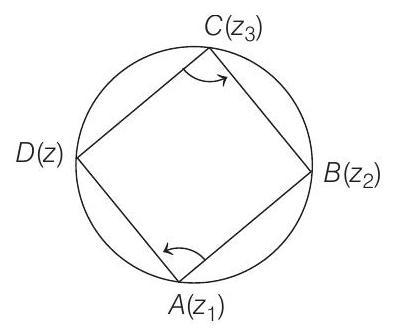
(c) For any two non-zero complex numbers $z_{1}$ and $z_{2}$ , $\arg \frac{z_{1}}{z_{2}} - \arg (z_{1}) + \arg (z_{2})$ is an integer multiple of $2 π$ .

(d) For any three given distinct complex numbers $z_{1}, z_{2}$ and $z_{3}$ , the locus of the point $z$ satisfying the condition $\arg \frac{(z - z_{1}) (z_{2} - z_{3})}{(z - z_{3}) (z_{2} - z_{1})} = π$ , lies on a straight line.

Show Answer

Answer:

Correct Answer: 8. $(a, b, d)$

Solution:

(a) Let

$z = - 1 - i and \arg (z) = θ$

Now, $\tan θ = \frac{im (z)}{Re (z)} = \frac{- 1}{- 1} = 1$

$\Rightarrow θ = \frac{π}{4}$

Since, $x < 0, y < 0$

$∴ \arg (z) = - π - \frac{π}{4} = - \frac{3 π}{4}$

(b) We have, $f (t) = \arg (- 1 + i t)$

$\arg (- 1 + i t) = \begin{matrix} π - \tan^{- 1} t, t \geq 0 \\ - (π + \tan^{- 1} t), t < 0 \end{matrix}$

This function is discontinuous at $t = 0$ .

$\begin{aligned} \arg \frac{z_{1}}{z_{2}} - \arg (z_{1}) + \arg (z_{2}) \\ Now, \arg \frac{z_{1}}{z_{2}} = \arg (z_{1}) - \arg (z_{2}) + 2 n π \\ ∴ \arg \frac{z_{1}}{z_{2}} - \arg (z_{1}) + \arg (z_{2}) \\ = \arg (z_{1}) - \arg (z_{2}) + 2 n π - \arg (z_{1}) + \arg (z_{2}) \\ = 2 n π \end{aligned}$

So, given expression is multiple of $2 π$ .

(d) We have, arg $\frac{(z - z_{1}) (z_{2} - z_{3})}{(z - z_{3}) (z_{2} - z_{1})} = π$

$\Rightarrow \frac{z - z_{1}}{z - z_{3}} \frac{z_{2} - z_{3}}{z_{2} - z_{1}}$ is purely real

Thus, the points $A (z_{1}), B (z_{2}), C (z_{3})$ and $D (z)$ taken in order would be concyclic if purely real.

Hence, it is a circle.

$∴$ (a), (b), (d) are false statement.

Complex Numbers 3 Question 8

8. For a non-zero complex number $z$ , let $\arg (z)$ denote the principal argument with $- π < \arg (z) \leq π$ . Then, which of the following statement(s) is (are) FALSE ? (2018 Adv.)

Answer:

Engineering Preparation

Medical Preparation

NCERT Books & Solutions

Important Resources

Other Resources

Syllabus

Test Platform

Sample Mock Test

Mentorship

NCERT Exercise Video Solution

Complex Numbers 3 Question 8

8. For a non-zero complex number z, let arg⁡(z) denote the principal argument with −π<arg⁡(z)≤π. Then, which of the following statement(s) is (are) FALSE ? (2018 Adv.)

Answer:

Engineering Preparation

Medical Preparation

NCERT Books & Solutions

Important Resources

Other Resources

Syllabus

Test Platform

Sample Mock Test

Mentorship

NCERT Exercise Video Solution

Menu

8. For a non-zero complex number $z$ , let $\arg (z)$ denote the principal argument with $- π < \arg (z) \leq π$ . Then, which of the following statement(s) is (are) FALSE ? (2018 Adv.)