Circle 5 Question 24
24. Two parallel chords of a circle of radius 2 are at a distance $\sqrt{3}+1$ apart. If the chords subtend at the centre, angles of $\pi / k$ and $\frac{2 \pi}{k}$, where $k>0$, then the value of $[k]$ is……
(2010)
NOTE $[k]$ denotes the largest integer less than or equal to $k]$
Show Answer
Answer:
Correct Answer: 24. 3
Solution:
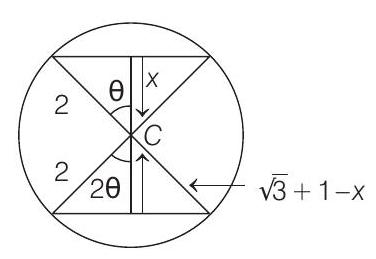
- Let
$$ \theta=\frac{\pi}{2 k} \quad \Rightarrow \quad \cos \theta=\frac{x}{2} $$
$\Rightarrow \quad \cos 2 \theta=\frac{\sqrt{3}+1-x}{2}$
$\Rightarrow \quad 2 \cos ^{2} \theta-1=\frac{\sqrt{3}+1-x}{2}$
$\Rightarrow \quad 2 \frac{x^{2}}{4}-1=\frac{\sqrt{3}+1-x}{2}$
$\Rightarrow x^{2}+x-3-\sqrt{3}=0$
$\Rightarrow x=\frac{-1 \pm \sqrt{1+12+4 \sqrt{3}}}{2}$
$=\frac{-1 \pm \sqrt{13+4 \sqrt{3}}}{2}=\frac{-1+2 \sqrt{3}+1}{2}=\sqrt{3}$
$\therefore \quad \cos \theta=\frac{\sqrt{3}}{2} \Rightarrow \theta=\frac{\pi}{6}$
$\therefore$ Required angle $=\frac{\pi}{k}=2 \theta=\frac{\pi}{3}$
$\Rightarrow \quad k=3$
Download Chapter Test http://tinyurl.com/y4wkkqkf or
