Circle 5 Question 19
19. Find the intervals of values of $a$ for which the line $y+x=0$ bisects two chords drawn from a point $\frac{1+\sqrt{2} a}{2}, \frac{1-\sqrt{2} a}{2}$ to the circle
$2 x^{2}+2 y^{2}-(1+\sqrt{2} a) x-(1-\sqrt{2} a) y=0$.
$(1996,6 M)$
Show Answer
Answer:
Correct Answer: 19. $a \in(-\infty,-2) \cup(2, \infty)$
Solution:
- Given, $2 x^{2}+2 y^{2}-(1+\sqrt{2} a) x-(1-\sqrt{2} a) y=0$
$\Rightarrow \quad x^{2}+y^{2}-\frac{1+\sqrt{2} a}{2} x-\frac{1-\sqrt{2} a}{2} y=0$
Since, $y+x=0$ bisects two chords of this circle, mid points of the chords must be of the form $(\alpha,-\alpha)$.
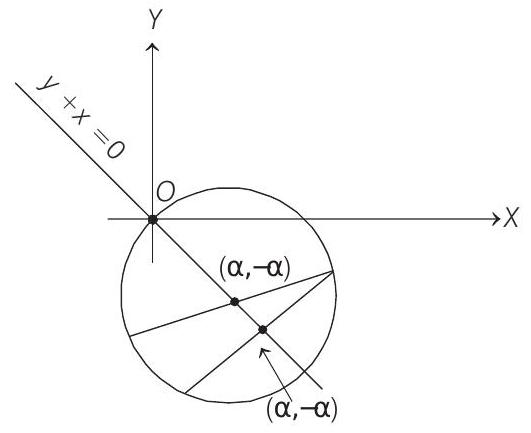
Equation of the chord having $(\alpha,-\alpha)$ as mid points is
$ T=S _1 $
$\Rightarrow x \alpha+y(-\alpha)-\frac{1+\sqrt{2} a}{4}(x+\alpha)-\frac{1-\sqrt{2} a}{4}(y-\alpha)$
$=\alpha^{2}+(-\alpha)^{2}-\frac{1+\sqrt{2} a}{2} \alpha-\frac{1-\sqrt{2} a}{2}(-\alpha)$
$\Rightarrow 4 x \alpha-4 y \alpha-(1+\sqrt{2} a) x-(1+\sqrt{2} a) \alpha$
$ -(1-\sqrt{2} a) y+(1-\sqrt{2} a) \alpha $
$ =4 \alpha^{2}+4 \alpha^{2}-(1+\sqrt{2} a) \cdot 2 \alpha+(1-\sqrt{2} a) \cdot 2 \alpha $
$\Rightarrow 4 \alpha x-4 \alpha y-(1+\sqrt{2} a) x-(1-\sqrt{2} \alpha) y$
$ =8 \alpha^{2}-(1+\sqrt{2} a) \alpha+(1-\sqrt{2} a) \alpha $
But this chord will pass through the point
$ \frac{1+\sqrt{2} a}{2}, \frac{1-\sqrt{2} a}{2} $
$4 \alpha \frac{1+\sqrt{2} a}{2}-4 \alpha \frac{1-\sqrt{2} a}{2}-\frac{(1+\sqrt{2} a)(1+\sqrt{2} a)}{2}$
$ -\frac{(1-\sqrt{2} a)(1-\sqrt{2} a)}{2} $
$=8 \alpha^{2}-2 \sqrt{2} \alpha \alpha$
$\Rightarrow \quad 2 \alpha[(1+\sqrt{2} a-1+\sqrt{2} \alpha)]=8 \alpha^{2}-2 \sqrt{2} a \alpha$
$\Rightarrow \quad 4 \sqrt{2} \alpha \alpha-\frac{1}{2}\left[2+2(\sqrt{2} a)^{2}\right]=8 \alpha^{2}-2 \sqrt{2} \alpha \alpha$
$\left[\because(a+b)^{2}+(a-b)^{2}=2 a^{2}+2 b^{2}\right]$
$\Rightarrow 8 \alpha^{2}-6 \sqrt{2} a \alpha+1+2 a^{2}=0$
But this quadratic equation will have two distinct roots, if
$ \begin{array}{ll} (6 \sqrt{2} a)^{2}-4(8)\left(1+2 a^{2}\right)>0 & \Rightarrow 72 a^{2}-32\left(1+2 a^{2}\right)>0 \\ \Rightarrow & 8 a^{2}-32>0 \\ \Rightarrow & \Rightarrow<-2 \cup a^{2}-4>0 \end{array} $
Therefore, $a \in(-\infty,-2) \cup(2, \infty)$.
