Circle 5 Question 17
17. Let $T _1, T _2$ and be two tangents drawn from $(-2,0)$ onto the circle $C: x^{2}+y^{2}=1$. Determine the circles touching $C$ and having $T _1, T _2$ as their pair of tangents. Further, find the equations of all possible common tangents to these circles when taken two at a time.
(1999, 10M)
Show Answer
Answer:
Correct Answer: 17. $x+\frac{4}{3}^{2}+y^{2}=\frac{1}{3}^{2} ; y= \pm \frac{5}{\sqrt{39}} \quad x+\frac{4}{5}$
Solution:
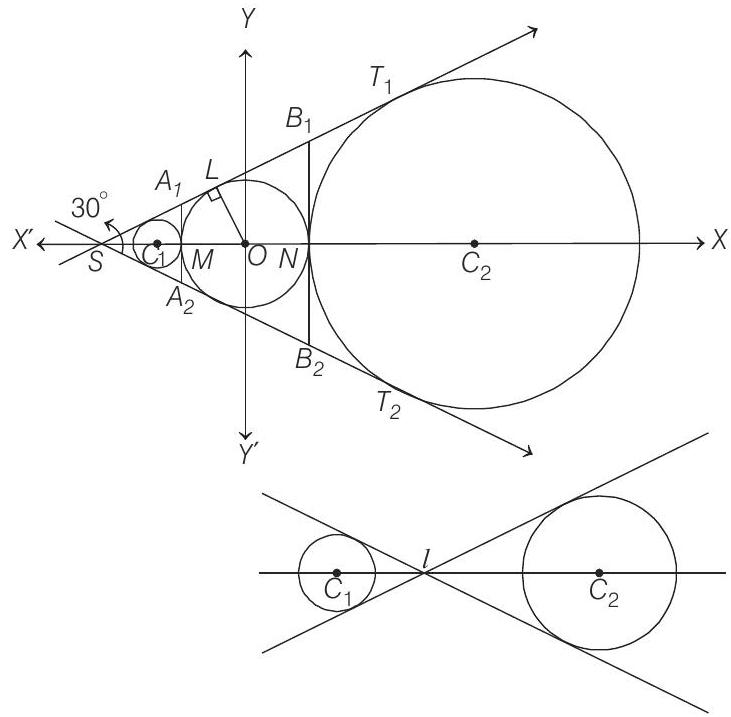
From figure it is clear that, $\triangle O L S$ is a right triangle with right angle at $L$.
Also,
$ O L=1 \text { and } O S=2 $
$\therefore 1 \sin (\angle L S O)=\frac{1}{2} \Rightarrow \angle L S O=30^{\circ}$
Since, $S A _1=S A _2, \Delta S A _1 A _2$ is an equilateral triangle.
The circle with centre at $C _1$ is a circle inscribed in the $\triangle S A _1 A _2$. Therefore, centre $C _1$ is centroid of $\triangle S A _1 A _2$. This, $C _1$ divides $S M$ in the ratio $2: 1$. Therefore, coordinates of $C _1$ are $(-4 / 3,0)$ and its radius $=C _1 M=1 / 3$
$\therefore$ Its equation is $(x+4 / 3)^{2}+y^{2}=(1 / 3)^{2}$
The other circle touches the equilateral triangle $S B _1 B _2$ externally. Its radius $r$ is given by $r=\frac{\Delta}{s-a}$,
where $B _1 B _2=a$. But $\Delta=\frac{1}{2}(a)(S N)=\frac{3}{2} a$
and
$ s-a=\frac{3}{2} a-a=\frac{a}{2} $
Thus,
$ r=3 $
$\Rightarrow$ Coordinates of $C _2$ are $(4,0)$
$\therefore$ Equation of circle with centre at $C _2$ is
$ (x-4)^{2}+y^{2}=3^{2} $
Equations of common tangents to circle (i) and circle $C$ are
$ x=-1 \quad \text { and } \quad y= \pm \frac{1}{\sqrt{3}}(x+2) \quad\left[T _1 \text { and } T _2\right] $
Equation of common tangents to circle (ii) and circle $C$ are
$ x=1 \quad \text { and } \quad y= \pm \frac{1}{\sqrt{3}}(x+2) \quad\left[T _1 \text { and } T _2\right] $
Two tangents common to (i) and (ii) are $T _1$ and $T _2$ at $O$. To find the remaining two transverse tangents to (i) and (ii), we find a point I which divides the joint of $C _1 C _2$ in the ratio $r _1: r _2=1 / 3: 3=1: 9$
Therefore, coordinates of I are $(-4 / 5,0)$
Equation of any line through I is $y=m(x+4 / 5)$. It will touch (i) if
$ \begin{aligned} & \frac{m \frac{-4}{3}+\frac{4}{5}-0}{\sqrt{1+m^{2}}}=\frac{1}{3} \Rightarrow-\frac{8 m}{15}=\frac{1}{3} \sqrt{1+m^{2}} \\ & \Rightarrow \quad 64 m^{2}=25\left(1+m^{2}\right) \\ & \Rightarrow \quad 39 m^{2}=25 \quad \Rightarrow \quad m= \pm \frac{5}{\sqrt{39}} \end{aligned} $
Therefore, these tangents are $y= \pm \frac{5}{\sqrt{39}} \quad x+\frac{4}{5}$
