Circle 5 Question 10
10. The equation of the locus of the mid-points of the chords of the circle $4 x^{2}+4 y^{2}-12 x+4 y+1=0$ that subtend an angle of $2 \pi / 3$ at its centre is … .
(1993, 2M)
Show Answer
Answer:
Correct Answer: 10. $16 x^{2}+16 y^{2}-48 x+16 y+31=0$
Solution:
- Given, $4 x^{2}+4 y^{2}-12 x+4 y+1=0$
$\Rightarrow \quad x^{2}+y^{2}-3 x+y+1 / 4=0$ whose centre is $\frac{3}{2},-\frac{1}{2}$ and radius
$ \begin{aligned} & =\sqrt{\frac{3}{2}^{2}+-\frac{1}{2}^{2}-\frac{1}{4}}=\sqrt{\frac{9}{4}+\frac{1}{4}-\frac{1}{4}} \\ & =\frac{3}{2} \end{aligned} $
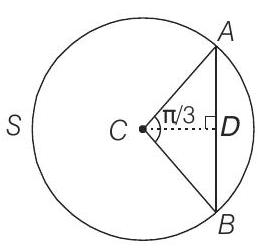
Again, let $S$ be a circle with centre at $C$ and $A B$ is given chord and $A D$ subtend angle $2 \pi / 3$ at the centre and $D$ be the mid point of $A B$ and let its coordinates are $(h, k)$.
Now, $\quad \angle D C A=\frac{1}{2}(\angle B C A)=\frac{1}{2} \cdot \frac{2 \pi}{3}=\frac{\pi}{3}$
Using sine rule in $\triangle A D C$,
$ \frac{D A}{\sin \pi / 3}=\frac{C A}{\sin \pi / 2} $
$\Rightarrow D A=C A \sin \pi / 3=\frac{3}{2} \cdot \frac{\sqrt{3}}{2}$
Now, in $\triangle A C D$
$ \begin{array}{ll} & C D^{2}=C A^{2}-A D^{2}=\frac{9}{4}-\frac{27}{16}=\frac{9}{16} \\ \text { But } & C D^{2}=(h-3 / 2)^{2}+(k+1 / 2)^{2} \\ \Rightarrow \quad & (h-3 / 2)^{2}+(k+1 / 2)^{2}=\frac{9}{16} \end{array} $
Hence, locus of a point is
$ \begin{aligned} x-\frac{3}{2}^{2}+y+\frac{1}{2}^{2} & =\frac{9}{16} \\ \Rightarrow \quad 16 x^{2}+16 y^{2}-48 x+16 y+31 & =0 \end{aligned} $
