Circle 5 Question 1
1. If the angle of intersection at a point where the two circles with radii $5 cm$ and $12 cm$ intersect is $90^{\circ}$, then the length (in cm) of their common chord is
(a) $\frac{13}{5}$
(b) $\frac{120}{13}$
(c) $\frac{60}{13}$
(d) $\frac{13}{2}$
Show Answer
Answer:
Correct Answer: 1. (b)
Solution:
- Let the length of common chord $=A B=2 A M=2 x$
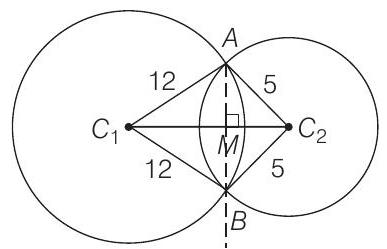
Now, $C _1 C _2=\sqrt{A C _1^{2}+A C _2^{2}}$
$\left[\because\right.$ circles intersect each other at $\left.90^{\circ}\right]$
$ \begin{aligned} & \text { and } C _1 C _2=C _1 M+M C _2 \\ & \Rightarrow \quad C _1 C _2=\sqrt{12^{2}-A M^{2}}+\sqrt{5^{2}-A M^{2}} \end{aligned} $
From Eqs. (i) and (ii), we get
$ \begin{aligned} & \sqrt{A C _1^{2}+A C _2^{2}}=\sqrt{144-A M^{2}}+\sqrt{25-A M^{2}} \\ & \Rightarrow \quad \sqrt{144+25}=\sqrt{144-x^{2}}+\sqrt{25-x^{2}} \\ & \Rightarrow \quad 13=\sqrt{144-x^{2}}+\sqrt{25-x^{2}} \end{aligned} $
On squaring both sides, we get
$ \begin{aligned} & 169=144-x^{2}+25-x^{2}+2 \sqrt{144-x^{2}} \sqrt{25-x^{2}} \\ & \Rightarrow \quad x^{2}=\sqrt{144-x^{2}} \sqrt{25-x^{2}} \end{aligned} $
Again, on squaring both sides, we get
$x^{4}=\left(144-x^{2}\right)\left(25-x^{2}\right)=(144 \times 25)-(25+144) x^{2}+x^{4}$
$\Rightarrow x^{2}=\frac{144 \times 25}{169} \Rightarrow x=\frac{12 \times 5}{13}=\frac{60}{13} cm$
Now, length of common chord $2 x=\frac{120}{13} cm$
Alternate Solution
Given, $A C _1=12 cm$ and $A C _2=5 cm$
In $\Delta C _1 A C _2$,
$ C _1 C _2=\sqrt{\left(C _1 A\right)^{2}+\left(A C _2\right)^{2}} \quad\left[\because \angle C _1 A C _2=90^{\circ},\right. $
because circles intersects each other at $90^{\circ}$ ]
$ =\sqrt{169}=13 cm $
$ =\sqrt{(12)^{2}+(5)^{2}}=\sqrt{144+25} $
Now, area of $\Delta C _1 A C _2=\frac{1}{2} A C _1 \times A C _2$
$ =\frac{1}{2} \times 12 \times 5=30 cm^{2} $
Also, area of $\Delta C _1 A C _2=\frac{1}{2} C _1 C _2 \times A M$
$ =\frac{1}{2} \times 13 \times \frac{A B}{2} \quad \because A M=\frac{A B}{2} $
$ \begin{aligned} \therefore \quad \frac{1}{4} \times 13 \times A M & =30 cm \\ A M & =\frac{120}{13} cm \end{aligned} $
