Circle 4 Question 21
21. Let a given line $L _1$ intersect the $X$ and $Y$-axes at $P$ and $Q$ respectively. Let another line $L _2$, perpendicular to $L _1$, cut the $X$ and $Y$-axes at $R$ and $S$, respectively. Show that the locus of the point of intersection of the line $P S$ and $Q R$ is a circle passing through the origin.
(1987, 3M)
Show Answer
Solution:
- Let the equation of $L _1$ be $x \cos \alpha+y \sin \alpha=p _1$.
Then, any line perpendicular to $L _1$ is
$x \sin \alpha-y \cos \alpha=p _2$
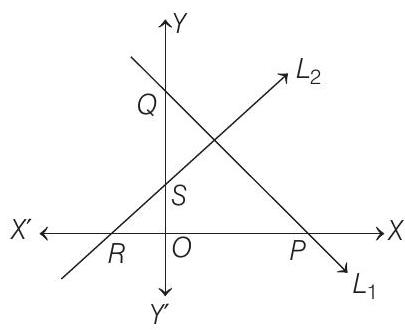
where, $p _2$ is a variable.
Then, $L _1$ meets $X$-axis at $P\left(p _1 \sec \alpha, 0\right)$ and $Y$-axis at $Q\left(0, p _1 \operatorname{cosec} \alpha\right)$.
Similarly, $L _2$ meets $X$-axis at $R\left(p _2 \operatorname{cosec} \alpha, 0\right)$ and $Y$-axis at $S\left(0,-p _2 \sec \alpha\right)$.
Now, equation of $P S$ is,
$ \frac{x}{p _1 \sec \alpha}+\frac{y}{-p _2 \sec \alpha}=1 \Rightarrow \frac{x}{p _1}-\frac{y}{p _2}=\sec \alpha $
Similarly, equation of $Q R$ is
$\frac{x}{p _2 \operatorname{cosec} \alpha}+\frac{y}{p _1 \operatorname{cosec} \alpha}=1 \Rightarrow \frac{x}{p _2}+\frac{y}{p _1}=\operatorname{cosec} \alpha$
Locus of point of intersection of $P S$ and $Q R$ can be obtained by eliminating the variable $p _2$ from Eqs. (i) and (ii).
$ \begin{aligned} & \therefore \quad \frac{x}{p _1}-\sec \alpha \frac{x}{y}+\frac{y}{p _1}=\operatorname{cosec} \alpha \\ & \Rightarrow \quad\left(x-p _1 \sec \alpha\right) x+y^{2}=p _1 y \operatorname{cosec} \alpha \\ & \Rightarrow x^{2}+y^{2}-p _1 x \sec \alpha-p _1 y \operatorname{cosec} \alpha=0 \\ & \text { which is a circle through origin. } \end{aligned} $
