Circle 4 Question 19
19. A circle touches the line
(1990, 5M)
Show Answer
Answer:
Correct Answer: 19.
Solution:
- The parametric form of
Since,
So, the coordinates of
So,
Let
Now,
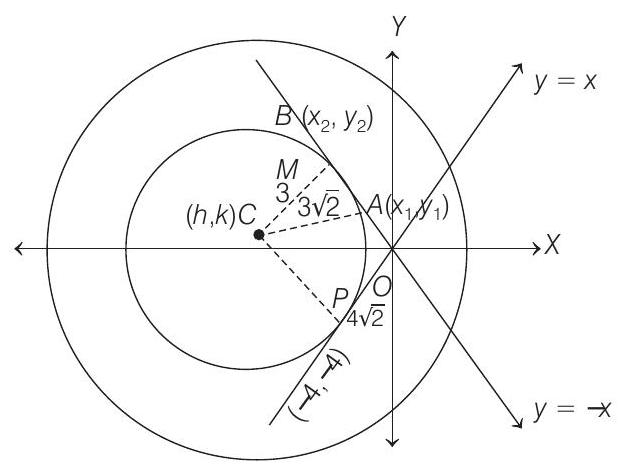
In
From Eqs. (i) and (iv), we get
Thus, the equation of the circles are
Clearly,
Hence, the required equation of circle, is






