Circle 3 Question 9
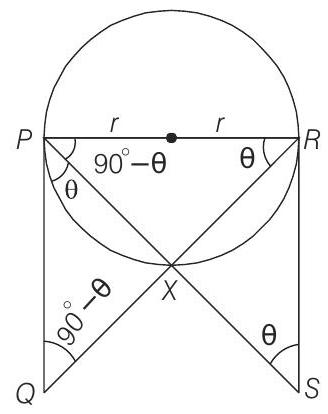
9. Let $P Q$ and $R S$ be tangents at the extremities of the diameter $P R$ of a circle of radius $r$. If $P S$ and $R Q$ intersect at a point $X$ on the circumference of the circle, then $2 r$ equals
(2001, 1M)
(a) $\sqrt{P Q \cdot R S}$
(b) $\frac{P Q+R S}{2}$
(c) $\frac{2 P Q \cdot R S}{P Q+R S}$
(d) $\sqrt{\frac{P Q^{2}+R S^{2}}{2}}$
Show Answer
Answer:
Correct Answer: 9. (a)
Solution:
- From figure, it is clear that $\triangle P R Q$ and $\triangle R S P$ are similar.
$ \begin{aligned} & \therefore \quad \frac{P R}{R S}=\frac{P Q}{R P} \\ & \Rightarrow \quad P R^{2}=P Q \cdot R S \\ & \Rightarrow \quad P R=\sqrt{P Q \cdot R S} \\ & \Rightarrow \quad 2 r=\sqrt{P Q \cdot R S} \end{aligned} $
