Circle 3 Question 22
22. Two circles, each of radius 5 units, touch each other at
Show Answer
Answer:
Correct Answer: 22. (
Solution:
- We have,
Slope of the common tangent
If
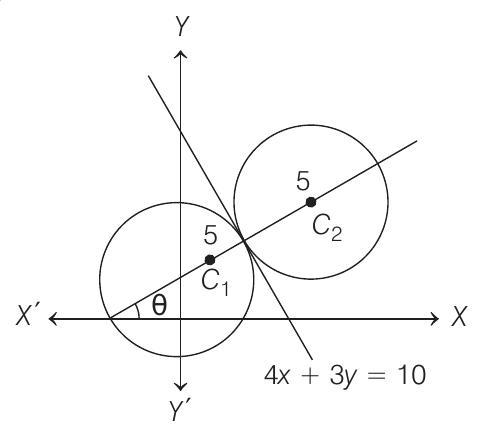
So, the equation of
Since,
So, the coordinates of
Thus, the coordinates of
Hence, the equations of the two circles are
and






