Circle 3 Question 14
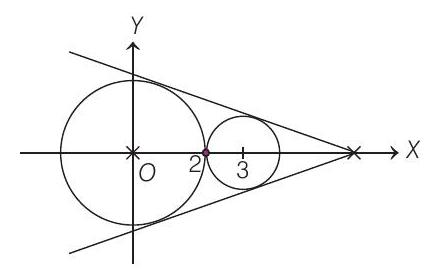
14. A common tangent of the two circles is
(a) $x=4$
(b) $y=2$
(c) $x+\sqrt{3} y=4$
(d) $x+2 \sqrt{2} y=6$
Passage 2
$A$ circle $C$ of radius 1 is inscribed in an equilateral $\triangle P Q R$. The points of contact of $C$ with the sides $P Q, Q R$, $R P$ are $D, E, F$ respectively. The line $P Q$ is given by the equation $\sqrt{3} x+y-6=0$ and the point $D$ is $\frac{3 \sqrt{3}}{2}, \frac{3}{2}$.
Further, it is given that the origin and the centre of $C$ are on the same side of the line $P Q$.
$(2008,12 M)$
Show Answer
Answer:
Correct Answer: 14. (d)
Solution:
- Here, equation of common tangent be
$ y=m x \pm 2 \sqrt{1+m^{2}} $
which is also the tangent to
$ \begin{aligned} & (x-3)^{2}+y^{2}=1 \\ & \Rightarrow \quad \frac{\left|3 m-0+2 \sqrt{1+m^{2}}\right|}{\sqrt{m^{2}+1}}=1 \\ & \Rightarrow \quad 3 m+2 \sqrt{1+m^{2}}= \pm \sqrt{1+m^{2}} \\ & \Rightarrow \quad 3 m=-3 \sqrt{1+m^{2}} \\ & \text { or } \quad 3 m=-\sqrt{1+m^{2}} \\ & \Rightarrow \quad m^{2}=1+m^{2} \text { or } 9 m^{2}=1+m^{2} \\ & \Rightarrow \quad m \in \varphi \text { or } m= \pm \frac{1}{2 \sqrt{2}} \\ & \therefore \quad y= \pm \frac{1}{2 \sqrt{2}} x \pm 2 \sqrt{1+\frac{1}{8}} \\ & \Rightarrow \quad y= \pm \frac{x}{2 \sqrt{2}} \pm \frac{6}{2 \sqrt{2}} \\ & \Rightarrow \quad 2 \sqrt{2} y= \pm(x+6) \\ & \therefore \quad x+2 \sqrt{2} y=6 \end{aligned} $
