Circle 2 Question 15
16. Let $T$ be the line passing through the points $P(-2,7)$ and $Q(2,-5)$. Let $F _1$ be the set of all pairs of circles $\left(S _1, S _2\right)$ such that $T$ is tangent to $S _1$ at $P$ and tangent to $S _2$ at $Q$, and also such that $S _1$ and $S _2$ touch each other at a point, say $M$. Let $E _1$ be the set representing the locus of $M$ as the pair $\left(S _1, S _2\right)$ varies in $F _1$. Let the set of all straight line segments joining a pair of distinct points of $E _1$ and passing through the point $R(1,1)$ be $F _2$. Let $E _2$ be the set of the mid-points of the line segments in the set $F _2$. Then, which of the following statement(s) is (are) TRUE?
(2018 Adv.)
(a) The point $(-2,7)$ lies in $E _1$
(b) The point $\frac{4}{5}, \frac{7}{5}$ does NOT lie in $E _2$
(c) The point $\frac{1}{2}, 1$ lies in $E _2$
(d) The point $0, \frac{3}{2}$ does NOT lie in $E _1$
Show Answer
Answer:
Correct Answer: 16. (a, d)
Solution:
- It is given that $T$ is tangents to $S _1$ at $P$ and $S _2$ at $Q$ and $S _1$ and $S _2$ touch externally at $M$.
$\therefore \quad M N=N P=N Q$
$\therefore$ Locus of $M$ is a circle having $P Q$ as its diameter of circle.
$\therefore \quad$ Equation of circle
$ \begin{array}{cc} & (x-2)(x+2)+(y+5)(y-7)=0 \\ \Rightarrow \quad & x^{2}+y^{2}-2 y-39=0 \end{array} $
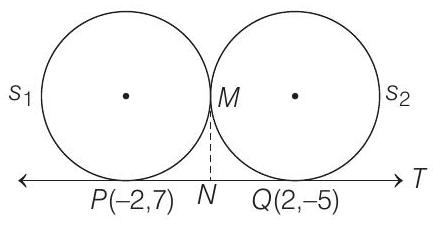
Hence, $\quad E _1: x^{2}+y^{2}-2 y-39=0, x \neq \pm 2$
Locus of mid-point of chord $(h, k)$ of the circle $E _1$ is $x h+y k-(y+k)-39=h^{2}+k^{2}-2 k-39$
$\Rightarrow x h+y k-y-k=h^{2}+k^{2}-2 k$
Since, chord is passing through $(1,1)$.
$\therefore \quad$ Locus of mid-point of chord $(h, k)$ is
$ \begin{array}{cc} & h+k-1-k=h^{2}+k^{2}-2 k \\ \Rightarrow \quad & h^{2}+k^{2}-2 k-h+1=0 \end{array} $
Locus is $E _2: x^{2}+y^{2}-x-2 y+1=0$
Now, after checking options, (a) and (d) are correct.
