Circle 1 Question 3
3. If a circle of radius $R$ passes through the origin $O$ and intersects the coordinate axes at $A$ and $B$, then the locus of the foot of perpendicular from $O$ on $A B$ is
(a) $\left(x^{2}+y^{2}\right)^{2}=4 R^{2} x^{2} y^{2}$
(b) $\left(x^{2}+y^{2}\right)^{3}=4 R^{2} x^{2} y^{2}$
(c) $\left(x^{2}+y^{2}\right)(x+y)=R^{2} x y$
(d) $\left(x^{2}+y^{2}\right)^{2}=4 R x^{2} y^{2}$
(2019 Main, 12 Jan II)
Show Answer
Answer:
Correct Answer: 3. (b)
Solution:
- Let the foot of perpendicular be $P(h, k)$. Then, the slope of line $O P=\frac{k}{h}$
$\because$ Line $A B$ is perpendicular to line $O P$, so slope of line
$ A B=-\frac{h}{k} $
$[\because$ product of slopes of two perpendicular lines is $(-1)$ ]
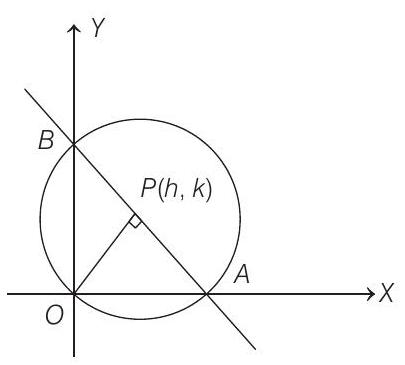
Now, the equation of line $A B$ is
$ \begin{aligned} & y-k=-\frac{h}{k}(x-h) \Rightarrow h x+k y=h^{2}+k^{2} \\ & \frac{x}{\frac{h^{2}+k^{2}}{h}}+\frac{y}{\frac{h^{2}+k^{2}}{k}}=1 \end{aligned} $
So, point $A \frac{h^{2}+k^{2}}{h}, 0$ and $B 0, \frac{h^{2}+k^{2}}{k}$
$\because \triangle A O B$ is a right angled triangle, so $A B$ is one of the diameter of the circle having radius $R$ (given).
$\Rightarrow A B=2 R$
$ \begin{aligned} & \Rightarrow \sqrt{\frac{h^{2}+k^{2}}{h}+\frac{h^{2}+k^{2}}{k}}=2 R \\ & \Rightarrow \quad\left(h^{2}+k^{2}\right)^{2} \frac{1}{h^{2}}+\frac{1}{k^{2}}=4 R^{2} \\ & \Rightarrow \quad\left(h^{2}+k^{2}\right)^{3}=4 R^{2} h^{2} k^{2} \end{aligned} $
On replacing $h$ by $x$ and $k$ by $y$, we get
$ \left(x^{2}+y^{2}\right)^{3}=4 R^{2} x^{2} y^{2}, $
which is the required locus.
