Circle 1 Question 25
25. Let
(a)
(b)
(c)
(d)
Show Answer
Solution:
- We have,
Let
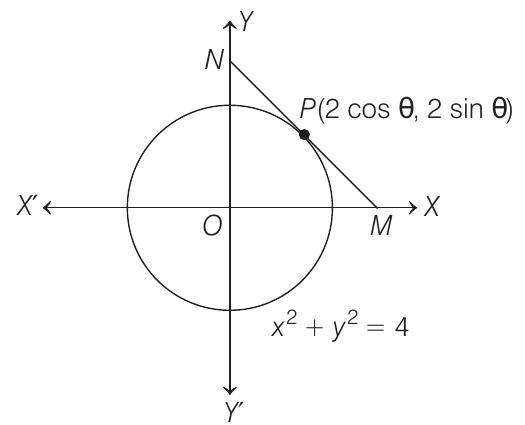
Let






