Area Question 8
Question 8
- The area of the region bounded by the curve $y=f(x)$, the $X$-axis and the lines $x=a$ and $x=b$, where $-\infty<a<b<-2$, is
(a) $\int_{a}^{b} \frac{x}{3\left[{f(x)}^{2}-1\right]} d x+b f(b)-a f(a)$
(b) $-\int_{a}^{b} \frac{x}{3\left[{f(x)}^{2}-1\right]} d x+b f(b)-a f(a)$
(c) $\int_{a}^{b} \frac{x}{3\left[{f(x)}^{2}-1\right]} d x-b f(b)+a f(a)$
(d) $-\int_{a}^{b} \frac{x}{3\left[{f(x)}^{2}-1\right]} d x-b f(b)+a f(a)$
Show Answer
Solution:
- Given, $y \leq x^{2}+3 x$
$\Rightarrow \quad y \leq x+\frac{3}{2}^{2}-\frac{9}{4} \Rightarrow x+\frac{3}{2}^{2} \geq y+\frac{9}{4}$
Since, $\quad 0 \leq y \leq 4$ and $0 \leq x \leq 3$
$\therefore$ The diagram for the given inequalities is
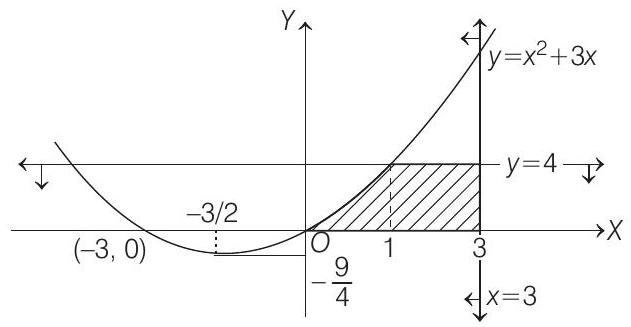
and points of intersection of curves $y=x^{2}+3 x$ and $y=4$ are $(1,4)$ and $(-4,4)$
Now required area
$=\int_{0}^{1}\left(x^{2}+3 x\right) d x+\int_{1}^{3} 4 d x=\frac{x^{3}}{3}+\frac{3 x^{2}}{2}{ }{0}^{1}+[4 x]{1}^{3}$
$=\frac{1}{3}+\frac{3}{2}+4(3-1)=\frac{2+9}{6}+8=\frac{11}{6}+8=\frac{59}{6}$ sq units
