Area Question 54
Question 54
- For any real $t, x=\frac{e^{t}+e^{-t}}{2}, y=\frac{e^{t}-e^{-t}}{2}$ is a point on the hyperbola $x^{2}-y^{2}=1$. Find the area bounded by this hrperbola and the lines joining its centre to the points corresponding to $t_{1}$ and $-t_{1}$.
$(1982,3 \mathrm{M})$
Show Answer
Solution:
- Let $P=\frac{e^{t_{1}}+e^{-t_{1}}}{2}, \frac{e^{t_{1}}-e^{-t_{1}}}{2}$
and $Q=\frac{e^{-t}+e^{t_{1}}}{2}, \frac{e^{-t_{1}}-e^{t}}{2}$
We have to find the area of the region bounded by the curve $x^{2}-y^{2}=1$ and the lines joining the centre $x=0$, $y=0$ to the points $\left(t_{1}\right)$ and $\left(-t_{1}\right)$.
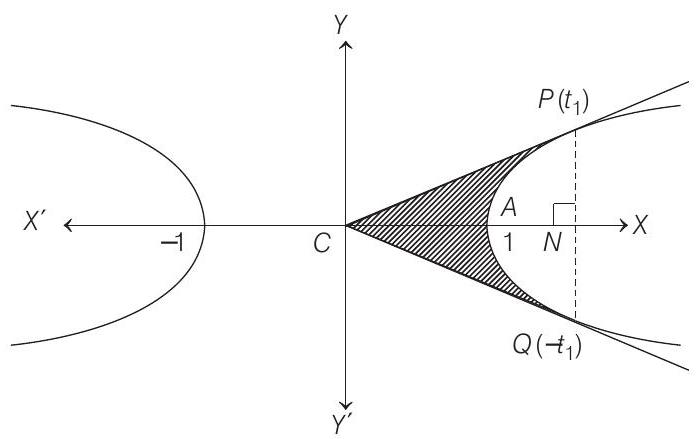
Required area
$$ \begin{aligned} & =2 \text { area of } \triangle P C N-\int_{1}^{\frac{e^{t_{1}}+e^{-t_{1}}}{2}} y d x \ & =2 \frac{1}{2} \frac{e^{t_{1}}+e^{-t_{1}}}{2} \frac{e^{t_{1}}-e^{-t_{1}}}{2}-\int_{1}^{t_{1}} y \frac{d y}{d t} \cdot d t \ & =2 \frac{e^{2 t_{1}}-e^{-2 t_{1}}}{8}-\int_{0}^{t_{1}} \frac{e^{t}-e^{-t}}{2} d t \ & =\frac{e^{2 t_{1}}-e^{-2 t_{1}}}{4}-\frac{1}{2} \int_{0}^{t_{1}}\left(e^{2 t}+e^{-2 t}-2\right) d t \ & =\frac{e^{2 t_{1}}-e^{-2 t_{1}}}{4}-\frac{1}{2} \frac{e^{2 t}}{2}-\frac{e^{-2 t}}{2}-2 t \ & =\frac{e^{2 t_{1}}-e^{-2 t_{1}}}{4}-\frac{1}{4}\left(e^{2 t_{1}}-e^{-2 t_{1}}-4 t_{1}\right) \end{aligned} $$
Download Chapter Test
