Area Question 48
Question 48
- Find the area bounded by the curves $x^{2}+y^{2}=25,4 y=\left|4-x^{2}\right|$ and $x=0$ above the $X$-axis.
$(1987,6 \mathrm{M})$
Show Answer
Solution:
- Given curves, $x^{2}+y^{2}=25,4 y=\left|4-x^{2}\right|$ could be sketched as below, whose points of intersection are
$$ x^{2}+\frac{\left(4-x^{2}\right)^{2}}{16}=25 $$
$$ \Rightarrow \quad\left(x^{2}+24\right)\left(x^{2}-16\right)=0 $$
$$ \Rightarrow \quad x= \pm 4 $$
$\therefore$ Required area $=2 \int_{0}^{4} \sqrt{25-x^{2}} d x-\int_{0}^{2} \frac{4-x^{2}}{4} d x$
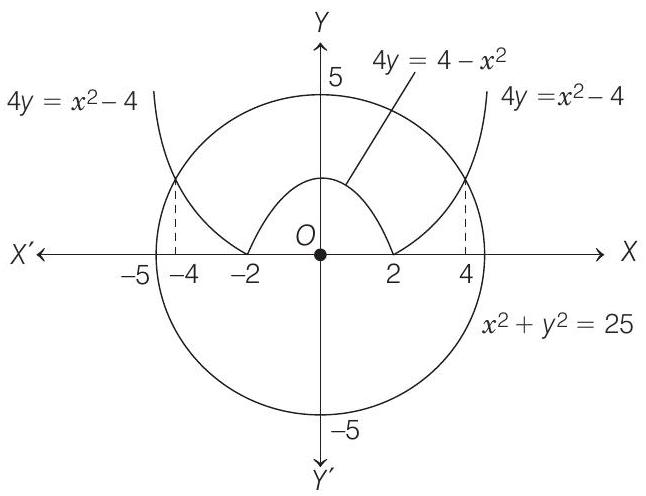
$$ \begin{gathered} -\int_{2}^{4} \frac{x^{2}-4}{4} d x \ =2 \frac{x}{2} \sqrt{25-x^{2}}+\frac{25}{2} \sin ^{-1} \frac{x}{5}{ }{0}^{4} \ -\frac{1}{4} 4 x-\frac{x^{3}}{3}{ }{0}^{2}-\frac{1}{4} \frac{x^{3}}{3}-4 x_{2}^{4} \end{gathered} $$
$=2 \quad 6+\frac{25}{2} \sin ^{-1} \frac{4}{5} \quad-\frac{1}{4} 8-\frac{8}{3}$
$$ -\frac{1}{4} \quad \frac{64}{3}-16-\frac{8}{3}-8 $$
$=2 \quad 6+\frac{25}{2} \sin ^{-1} \frac{4}{5}-\frac{4}{3}-\frac{4}{3}-\frac{4}{3}$
$=4+25 \sin ^{-1} \frac{4}{5}$ sq units
