Area Question 45
Question 45
- Compute the area of the region bounded by the curves $y=e x \log x$ and $y=\frac{\log x}{e x}$, where $\log e=1$.
$(1990,4$ M)
Show Answer
Solution:
- Both the curves are defined for $x>0$.
Both are positive when $x>1$ and negative when $0<x<1$. We know that, $\lim _{x \rightarrow 0^{+}}(\log x) \rightarrow-\infty$
Hence, $\lim _{x \rightarrow 0^{+}} \frac{\log x}{e x} \rightarrow-\infty$. Thus, $Y$-axis is asymptote of second curve.
$$ \begin{aligned} & \text { And } \lim _{x \rightarrow 0^{+}} e x \log x \ & =\lim _{x \rightarrow 0^{+}} \frac{e \log x}{1 / x} \ & =\lim _{x \rightarrow 0^{+}} \frac{e \frac{1}{x}}{-\frac{1}{x^{2}}}=0 \end{aligned} $$
Thus, the first curve starts from $(0,0)$ but does not include $(0,0)$.
Now, the given curves intersect, therefore
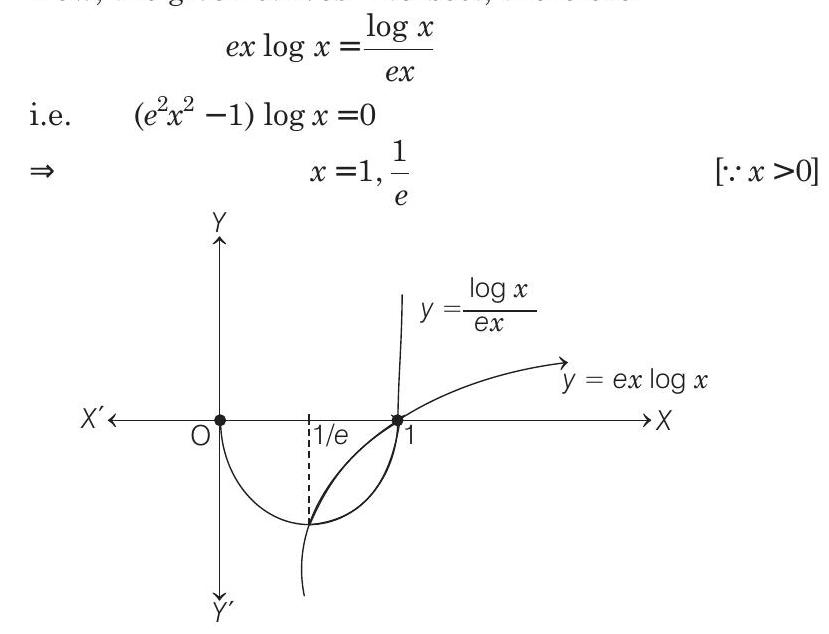$\therefore \quad$ The required area
$=\int_{1 / e}^{1} \frac{(\log x)}{e x}-e x \log x d x$
$=\frac{1}{e}{\frac{(\log x)^{2}}{2}}{1 / e}^{1}-e \frac{x^{2}}{4}(2 \log x-1){ }{1 / e}^{1}=\frac{e^{2}-5}{4 e}$ squnits
