Area Question 43
Question 43
- Sketch the region bounded by the curves $y=x^{2}$ and $y=2 /\left(1+x^{2}\right)$. Find its area.
$(1992,4$ M)
Show Answer
Solution:
- The curve $y=x^{2}$ is a parabola. It is symmetric about $Y$-axis and has its vertex at $(0,0)$ and the curve $y=\frac{2}{1+x^{2}}$ is a bell shaped curve. $X$-axis is its asymptote and it is symmetric about $Y$-axis and its vertex is $(0,2)$.
$$ \begin{aligned} & \text { Since, } \quad y=x^{2} \ & \text { and } \quad y=\frac{2}{1+x^{2}} \ & \Rightarrow \quad y=\frac{2}{1+y} \ & \Rightarrow \quad y^{2}+y-2=0 \ & \Rightarrow \quad(y-1)(y+2)=0 \Rightarrow y=-2,1 \ & \text { But } \quad y \geq 0 \text {, so } y=1 \Rightarrow x= \pm 1 \end{aligned} $$
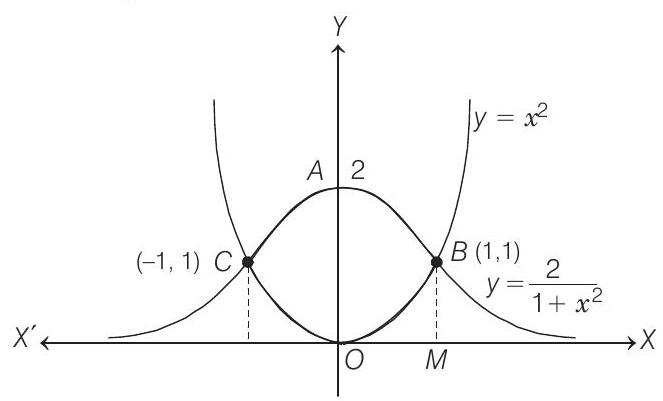
Therefore, coordinates of $C$ are $(-1,1)$ and coordinates of $B$ are $(1,1)$.
$\therefore$ Required area $O B A C O=2 \times$ Area of curve $O B A O$
$=2 \int_{0}^{1} \frac{2}{1+x^{2}} d x-\int_{0}^{1} x^{2} d x$
$=2\left[2 \tan ^{-1} x\right]{0}^{1}-{\frac{x^{3}}{3}}{0}^{1}=2 \frac{2 \pi}{4}-\frac{1}{3}=\pi-\frac{2}{3}$ sq unit
