Area Question 42
Question 42
- In what ratio, does the $X$-axis divide the area of the region bounded by the parabolas $y=4 x-x^{2}$ and $y=x^{2}-x ?$
$(1994,5$ M)
Show Answer
Solution:
- Given parabolas are $y=4 x-x^{2}$
and
$$ y=-(x-2)^{2}+4 $$
or
$$ (x-2)^{2}=-(y-4) $$
Therefore, it is a vertically downward parabola with vertex at $(2,4)$ and its axis is $x=2$
and
$$ y=x^{2}-x \Rightarrow y=x-\frac{1}{2} \quad-\frac{1}{4} $$
$$ \Rightarrow \quad x-\frac{1}{2}^{2}=y+\frac{1}{4} $$
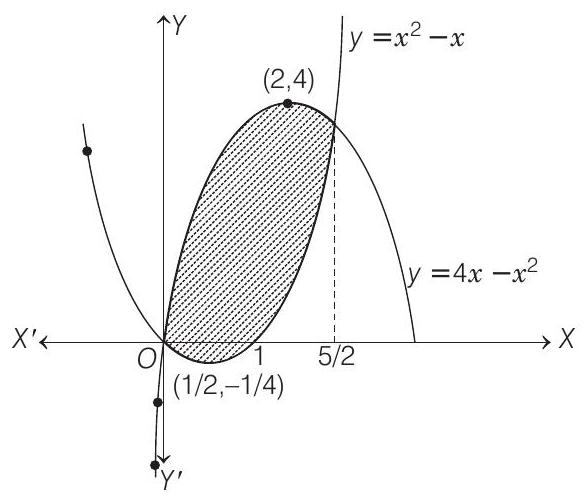
This is a parabola having its vertex at $\frac{1}{2},-\frac{1}{4}$.
Its axis is at $x=\frac{1}{2}$ and opening upwards.
The points of intersection of given curves are
$$ \begin{aligned} & 4 x-x^{2}=x^{2}-x \Rightarrow 2 x^{2}=5 x \ & \Rightarrow \quad x(2-5 x)=0 \quad \Rightarrow \quad x=0, \frac{5}{2} \end{aligned} $$
Also, $y=x^{2}-x$ meets $X$-axis at $(0,0)$ and $(1,0)$.
$\therefore$ Area, $A_{1}=\int_{0}^{5 / 2}\left[\left(4 x-x^{2}\right)-\left(x^{2}-x\right)\right] d x$
$$ \begin{aligned} & =\int_{0}^{5 / 2}\left(5 x-2 x^{2}\right) d x \ & =\frac{5}{2} x^{2}-\frac{2}{3} x^{3}{ }_{0}^{5 / 2}=\frac{5}{2} \frac{5}{2}^{2}-\frac{2}{3} \cdot \frac{5}{2}^{3} \ & =\frac{5}{2} \cdot \frac{25}{4}-\frac{2}{3} \cdot \frac{125}{8} \ & =\frac{125}{8} 1-\frac{2}{3}=\frac{125}{24} \text { sq units } \end{aligned} $$
This area is considering above and below $X$-axis both. Now, for area below $X$-axis separately, we consider
$$ A_{2}=-\int_{0}^{1}\left(x^{2}-x\right) d x=\frac{x^{2}}{2}-\frac{x^{3}}{3}{ }_{0}^{1}=\frac{1}{2}-\frac{1}{3}=\frac{1}{6} \text { sq units } $$
Therefore, net area above the $X$-axis is
$$ A_{1}-A_{2}=\frac{125-4}{24}=\frac{121}{24} \text { sq units } $$
Hence, ratio of area above the $X$-axis and area below $X$-axis
$$ =\frac{121}{24}: \frac{1}{6}=121: 4 $$
