Area Question 4
Question 4
- The area (in sq units) of the region $A=(x, y): \frac{y^{2}}{2} \leq x \leq y+4$ is
(2019 Main, 9 April II) (a) 30 (b) $\frac{53}{3}$ (c) 16 (d) 18
Show Answer
Solution:
- Given region $A=(x, y): \frac{y^{2}}{2} \leq x \leq y+4$
$$ \therefore \quad \frac{y^{2}}{2}=x $$
$$ \Rightarrow \quad y^{2}=2 x $$
and $x=y+4 \Rightarrow y=x-4$
Graphical representation of $A$ is
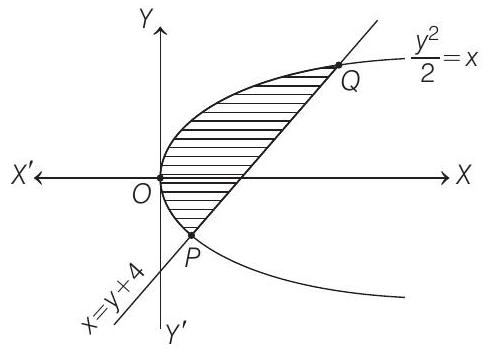
On substituting $y=x-4$ from Eq. (ii) to Eq. (i), we get
$$ \begin{array}{rlrl} & & (x-4)^{2} & =2 x \ \Rightarrow & & x^{2}-8 x+16 & =2 x \ \Rightarrow & & x^{2}-10 x+16 & =0 \ \Rightarrow & & (x-2)(x-8) & =0 \ \Rightarrow & & x & =2,8 \ \therefore & y & =-2,4 \end{array} $$
[from Eq. (ii)]
So, the point of intersection of Eqs. (i) and
(ii) are $P(2,-2)$ and $Q(8,4)$.
Now, the area enclosed by the region $A$
$$ \begin{aligned} & =\int_{-2}^{4}(y+4)-\frac{y^{2}}{2} d y=\frac{y^{2}}{2}+4 y-{\frac{y^{3}}{6}}_{-2}^{4} \ & =\frac{16}{2}+16-\frac{64}{6}-\frac{4}{2}-8+\frac{8}{6} \ & =8+16-\frac{32}{3}-2+8-\frac{4}{3} \ & =30-12=18 \text { sq unit. } \end{aligned} $$
