Area Question 38
Question 38
- $\operatorname{Let} f(x)=\max \left{x^{2},(1-x)^{2}, 2 x(1-x)\right}$, where $0 \leq x \leq 1$.
Determine the area of the region bounded by the curves $y=f(x), X$-axis, $x=0$ and $x=1$.
$(1997,5$ M)
Show Answer
Solution:
- We can draw the graph of $y=x^{2}, y=\left(1-x^{2}\right)$ and $y=2 x(1-x)$ in following figure
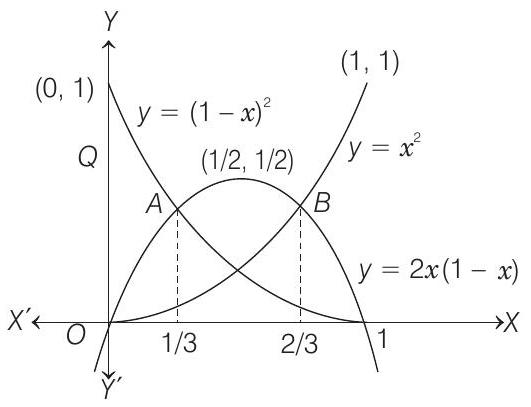
Now, to get the point of intersection of $y=x^{2}$ and $y=2 x(1-x)$, we get
$$ \begin{aligned} & & x^{2} & =2 x(1-x) \ \Rightarrow & & 3 x^{2} & =2 x \ \Rightarrow & & x(3 x-2) & =0 \ \Rightarrow & & x & =0,2 / 3 \end{aligned} $$
Similarly, we can find the coordinate of the points of intersection of
$$ y=\left(1-x^{2}\right) \text { and } y=2 x(1-x) \text { are } x=1 / 3 \text { and } x=1 $$
From the figure, it is clear that,
$$ \begin{array}{cc} (1-x)^{2}, & \text { if } 0 \leq x \leq 1 / 3 \ f(x)=2 x(1-x), & \text { if } 1 / 3 \leq x \leq 2 / 3 \ x^{2}, & \text { if } 2 / 3 \leq x \leq 1 \end{array} $$
$\therefore$ The required area
$$ \begin{aligned} A & =\int_{0}^{1} f(x) d x \ & =\int_{0}^{1 / 3}(1-x)^{2} d x+\int_{1 / 3}^{2 / 3} 2 x(1-x) d x+\int_{2 / 3}^{1} x^{2} d x \ & =-\frac{1}{3}(1-x)^{3}+x^{2}-{\frac{2 x^{3}}{3}}^{2 / 3}+\frac{1}{3} x^{3} \ & =-\frac{1}{3} \frac{2}{3}^{3}+\frac{1}{3}+\frac{2}{3}^{2}-\frac{2}{3} \frac{2}{3}^{3}-\frac{1}{3}^{2}+\frac{2}{3} \frac{1}{3}^{3} \ & +\frac{1}{3}(1)-\frac{1}{3} \frac{2^{3}}{3} \end{aligned} $$
$$ =\frac{19}{81}+\frac{13}{81}+\frac{19}{81}=\frac{17}{27} \text { sq unit } $$
