Area Question 37
Question 37
- Let
Show Answer
Solution:
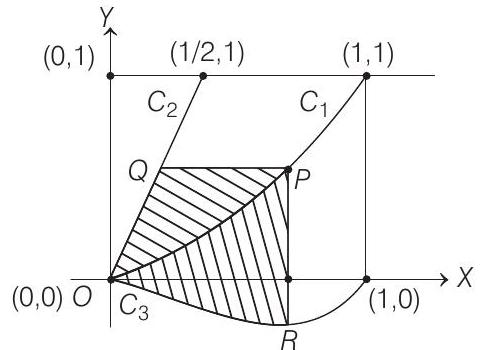
- Refer to the figure given in the question. Let the coordinates of
For the area
Upper boundary:
lower boundary :
Lower limit of
Upper limit of
For the area
The upper curve :
and the lower curve :
Lower limit of
and upper limit of
$$ \begin{aligned} \therefore \text { Area }(O P Q O) & =\int_{0}^{x^{2}} \sqrt{t} d t-\int_{0}^{x^{2}} \frac{t}{2} d t \ & =\frac{2}{3}\left[t^{3 / 2}\right]{0}^{x^{2}}-\frac{1}{4}\left[t^{2}\right]{0}^{x^{2}} \ & =\frac{2}{3} x^{3}-\frac{x^{4}}{4} \end{aligned} $$
According to the given condition,
On differentiating both sides w.r.t.






