Area Question 36
Question 36
- If $f(x)$ is a continuous function given by
$$ f(x)=\begin{array}{ll} 2 x, & |x| \leq 1 \ x^{2}+a x+b, & |x|>1 \end{array} $$
Then, find the area of the region in the third quadrant bounded by the curves $x=-2 y^{2}$ and $y=f(x)$ lying on the left on the line $8 x+1=0$.
$(1999,5$ M)
Show Answer
Solution:
- Given, $f(x)=\begin{aligned} & 2 x, \ & x^{2}+a x+b,|x|>1\end{aligned}$
$$ \Rightarrow \quad f(x)=\begin{array}{ll} x^{2}+a x+b, & \text { if } x<-1 \ 2 x, & \text { if }-1 \leq x<1 \ x^{2}+a x+b, & \text { if } x \geq 1 \end{array} $$
$f$ is continuous on $R$, so $f$ is continuous at -1 and 1 .
$$ \begin{aligned} & \lim _{x \rightarrow-1^{-}} f(x)=\lim _{x \rightarrow-1^{+}} f(x)=f(-1) \ & \text { and } \quad \lim _{x \rightarrow 1^{-}} f(x)=\lim _{x \rightarrow 1^{+}} f(x)=f(1) \ & \Rightarrow \quad 1-a+b=-2 \text { and } 2=1+a+b \ & \Rightarrow \quad a-b=3 \text { and } \quad a+b=1 \ & \therefore \quad a=2, \quad b=-1 \ & \text { Hence, } f(x)=\begin{array}{llc} x^{2}+2 x-1, & \text { if } & x<-1 \ 2 x, & \text { if } & -1 \leq x<1 \ x^{2}+2 x-1, & \text { if } & x \geq 1 \end{array} \end{aligned} $$
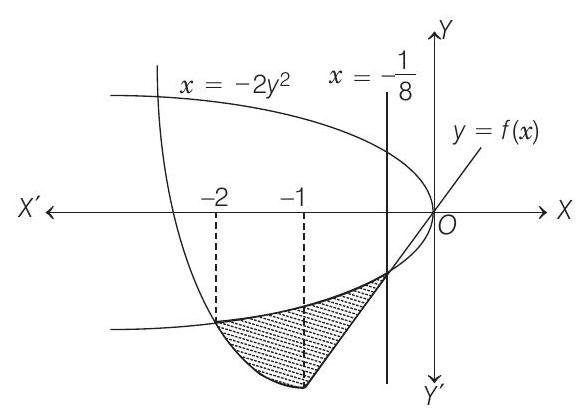
Next, we have to find the points $x=-2 y^{2}$ and $y=f(x)$. The point of intersection is $(-2,-1)$.
$\therefore \quad$ Required area $=\int_{-2}^{-1 / 8} \sqrt{\frac{-x}{2}}-f(x) d x$
$$ \begin{aligned} & =\int_{-2}^{-1 / 8} \sqrt{\frac{-x}{2}} d x-\int_{-2}^{-1}\left(x^{2}+2 x-1\right) d x-\int_{-1}^{-1 / 8} 2 x d x \ & =-\frac{2}{3 \sqrt{2}}\left[(-x)^{3 / 2}\right]{-2}^{-1 / 8}-\frac{x^{3}}{3}+x^{2}-x-{-2}^{-\left[x^{2}\right]_{-1}^{-1 / 8}} \ & =-\frac{2}{3 \sqrt{2}} \frac{1^{3 / 2}}{8}-2^{3 / 2}–\frac{1}{3}+1+1 \ & +-\frac{8}{3}+4+2-\frac{1}{64}-1 \ & =\frac{\sqrt{2}}{3}\left[2 \sqrt{2}-2^{-9 / 2}\right]+\frac{5}{3}+\frac{63}{64} \ & =\frac{63}{16 \times 3}+\frac{509}{64 \times 3}=\frac{761}{192} \text { squnits } \end{aligned} $$
