Area Question 31
Question 31
- For which of the following values of $m$, is the area of the region bounded by the curve $y=x-x^{2}$ and the line $y=m x$ equals $\frac{9}{2}$ ?
$(1999,3 \mathrm{M})$ (a) -4 (b) -2 (c) 2 (d) 4
Analytical & Descriptive Questions
$f(x)$ is a quadratic function and its maximum value occurs at a point $V$. $A$ is a point of intersection of $y=f(x)$ with $X$-axis and point $B$ is such that chord $A B$ subtends a right angle at $V$. Find the area enclosed by $f(x)$ and chord $A B$.
$(2005,5$ M)
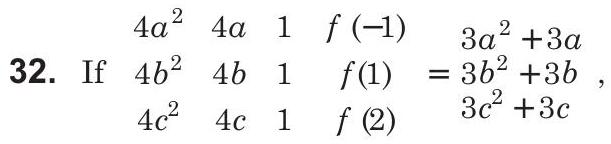
Show Answer
Solution:
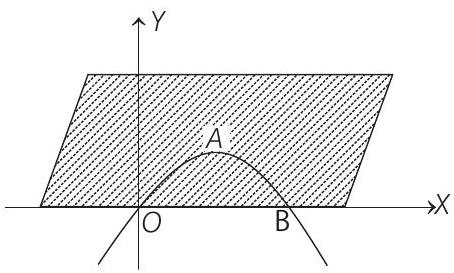
- Case I When $m=0$
In this case, $\quad y=x-x^{2}$
and
$y=0$
are two given curves, $y>0$ is total region above $X$-axis.
Therefore, area between $y=x-x^{2}$ and $y=0$
is area between $y=x-x^{2}$ and above the $X$-axis
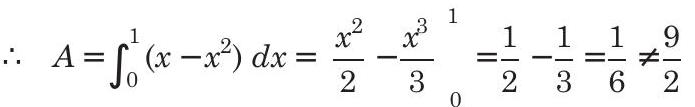
Hence, no solution exists.
Case II When $m<0$
In this case, area between $y=x-x^{2}$ and $y=m x$ is $O A B C O$ and points of intersection are $(0,0)$ and ${1-m, m(1-m)}$.
$\therefore \quad$ Area of curve $O A B C O=\int_{0}^{1-m}\left[x-x^{2}-m x\right] d x$
$$ \begin{array}{rlrl} & =(1-m) \frac{x^{2}}{2}-{\frac{x^{3}}{3}}^{1-m} \ & =\frac{1}{2}(1-m)^{3}-\frac{1}{3}(1-m)^{3}=\frac{1}{6}(1-m)^{3} \ \therefore \quad & \frac{1}{6}(1-m)^{3} & =\frac{9}{2} \ \Rightarrow \quad(1-m)^{3} & =27 \ \Rightarrow \quad 1-m & =3 \ \Rightarrow \quad & m & =-2 \end{array} $$
326 Area
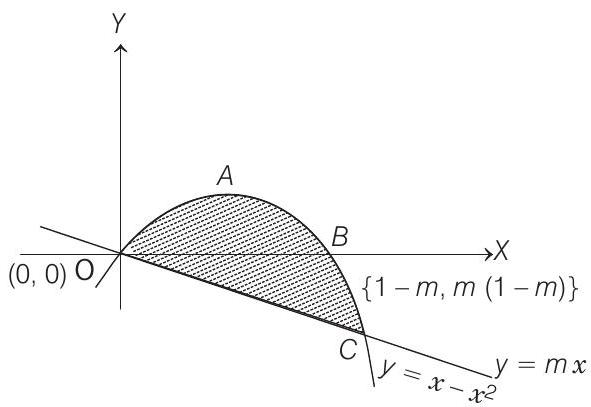
Case III When $m>0$
In this case, $y=m x$ and $y=x-x^{2}$ intersect in $(0,0)$ and ${(1-m), m(1-m)}$ as shown in figure
$\therefore$ Area of shaded region $=\int_{1-m}^{0}\left(x-x^{2}-m x\right) d x$
$$ \begin{aligned} & =(1-m) \frac{x^{2}}{2}-{\frac{x^{3}}{3}}^{0} \ & =-\frac{1}{2}(1-m)(1-m)^{2}+\frac{1}{3}(1-m)^{3} \ & =-\frac{1}{6}(1-m)^{3} \ \Rightarrow \quad \frac{9}{2} & =-\frac{1}{6}(1-m)^{3} \ \Rightarrow \quad(1-m)^{3} & =-27 \ \Rightarrow \quad(1-m) & =-3 \ \Rightarrow \quad m & =3+1=4 \end{aligned} $$
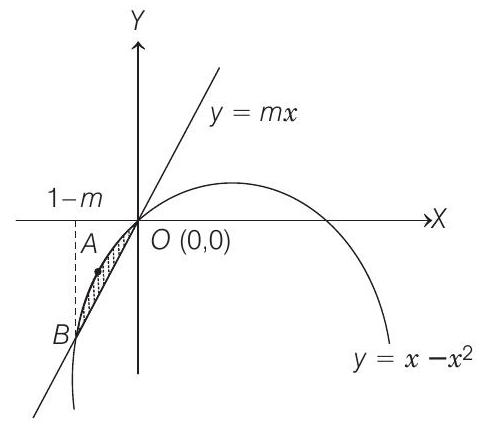
[given]
Therefore, (b) and (d) are the answers.
$$ \begin{array}{rrr} \Rightarrow \quad 4 a^{2} f(-1)+4 a f(1)+f(2) & =3 a^{2}+3 a, \ & 4 b^{2} f(-1)+4 b f(1)+f(2)=3 b^{2}+3 b \ \text { and } \quad 4 c^{2} f(-1)+4 c f(1)+f(2) & =3 c^{2}+3 c \end{array} $$
where, $f(x)$ is quadratic expression given by,
$$ f(x)=a x^{2}+b x+c \text { and Eqs. (i), (ii) and (iii). } $$
$\Rightarrow \quad 4 x^{2} f(-1)+4 x f(1)+f(2)=3 x^{2}+3 x$
or ${4 f(-1)-3} x^{2}+{4 f(1)-3} x+f(2)=0$
As above equation has 3 roots $a, b$ and $c$.
So, above equation is identity in $x$.
i.e. coefficients must be zero.
$$ \begin{array}{rrrl} \Rightarrow & f(-1) & =3 / 4, f(1)=3 / 4, f(2)=0 \ & \because & f(x) & =a x^{2}+b x+c \ \therefore & a=-1 / 4, b & =0 \text { and } c=1 \text {, using Eq. (v) } \end{array} $$
Thus, $\quad f(x)=\frac{4-x^{2}}{4}$ shown as,
Let $A(-2,0), B=\left(2 t,-t^{2}+1\right)$
Since, $A B$ subtends right angle at vertex $V(0,1)$.
$$ \Rightarrow \quad \frac{1}{2} \cdot \frac{t^{2}}{2 t}=-1 $$
$$ \begin{array}{lc} \Rightarrow & t=4 \ \therefore & B(8,-15) \end{array} $$
So, equation of chord $A B$ is $y=\frac{-(3 x+6)}{2}$.
$\therefore$ Required area $=\left|\int_{-2}^{8} \frac{4-x^{2}}{4}+\frac{3 x+6}{2} d x\right|$
$$ \begin{aligned} & =\left|x-\frac{x^{3}}{12}+\frac{3 x^{2}}{4}+3 x_{-2}^{8}\right| \ & =\mid 8-\frac{128}{3}+48+24–2+\frac{2}{3}+3-6 \ & =\frac{125}{3} \text { sq units } \end{aligned} $$
