Area Question 3
Question 3
- The area (in sq units) of the region bounded by the curves
Show Answer
Solution:
- Given, equations of curves
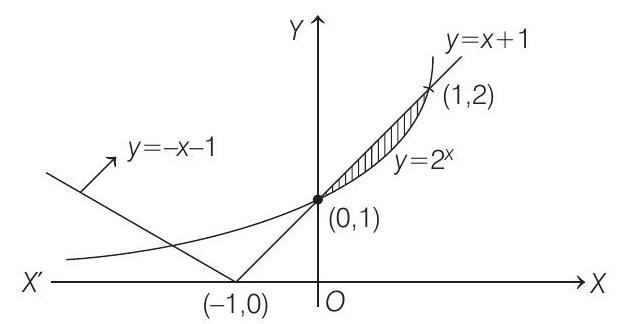
In first quadrant, the above given curves intersect each other at
So, the required area
$$ \begin{aligned} & =\frac{x^{2}}{2}+x-\frac{2^{x}}{\log {e} 2}{ }{0}^{1} \quad \because \int a^{x} d x=\frac{a^{x}}{\log _{e} a}+C \ & =\frac{1}{2}+1-\frac{2}{\log _{e} 2}+\frac{1}{\log _{e} 2} \ & =\frac{3}{2}-\frac{1}{\log _{e} 2} \end{aligned} $$






