Area Question 27
Question 27
- The slope of tanget to a curve $y=f(x)$ at $[x, f(x)]$ is $2 x+1$. If the curve passes through the point $(1,2)$, then the area bounded by the curve, the X-axis and the line $x=1$ is (a) $\frac{3}{2}$ (b) $\frac{4}{3}$ (c) $\frac{5}{6}$ (d) $\frac{1}{12}$
Objective Questions II
(One or more than one correct option)
Show Answer
Solution:
- Given, $\frac{d y}{d x}=2 x+1$
On integrating both sides
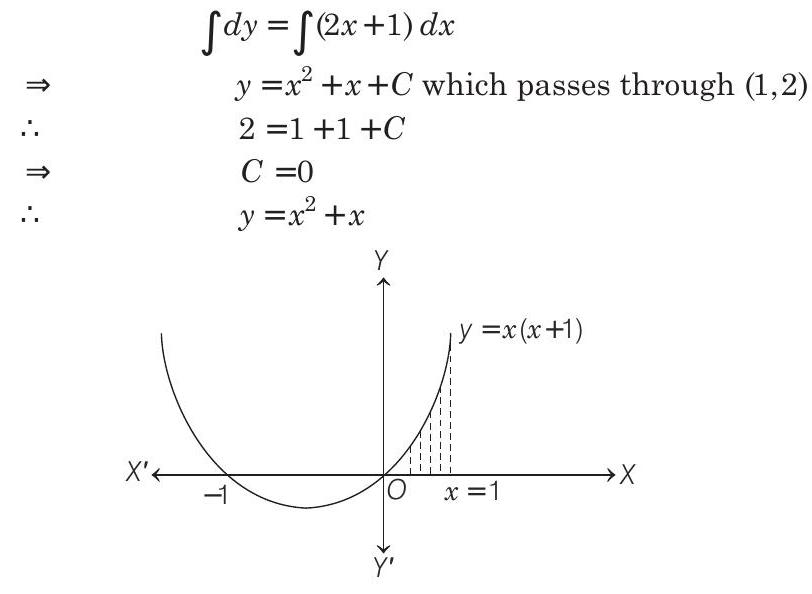
Thus, the required area bounded by $X$-axis, the curve and $x=1$
$$ \begin{aligned} & =\int_{0}^{1}\left(x^{2}+x\right) d x=\frac{x^{3}}{3}+\frac{x^{2}}{2} \ & =\frac{1}{3}+\frac{1}{2}=\frac{5}{6} \text { sq unit } \end{aligned} $$
