SATHEE: Area Question 25

Area Question 25

Question 25

The area enclosed between the curves $y = a x^{2}$ and $x = a y^{2} (a > 0)$ is 1 sq unit. Then, the value of $a$ is (a) $\frac{1}{\sqrt{3}}$ (b) $\frac{1}{2}$ (c) 1 (d) $\frac{1}{3}$

(2004, 1M)

Show Answer

Solution:

As from the figure, area enclosed between the curves is $O A B C O$ .

Thus, the point of intersection of

$y = a x^{2} and x = a y^{2}$

$\begin{array}{ll} \Rightarrow & x = a {(a x^{2})}^{2} \Rightarrow & x = 0, \frac{1}{a} \Rightarrow y = 0, \frac{1}{a} \end{array}$

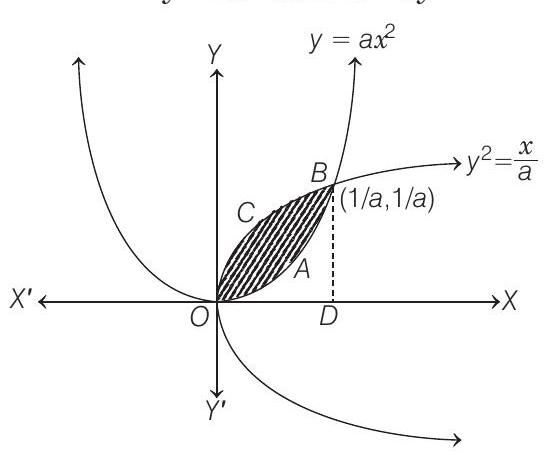
So, the points of intersection are $(0, 0)$ and $\frac{1}{a}, \frac{1}{a}$ .

$∴$ Required area $O A B C O =$ Area of curve $O C B D O$

Area of curve $O A B D O$

$\begin{aligned} \Rightarrow & \int_{0}^{1 / a} \sqrt{\frac{x}{a}} - a x^{2} d x & = 1 \Rightarrow & \frac{1}{\sqrt{a}} \cdot \frac{x^{3 / 2}}{3 / 2} - \frac{a x^{3}}{3}^{1 / a} & = 1 \Rightarrow & \frac{2}{3 a^{2}} - \frac{1}{3 a^{2}} & = 1 & a^{2} & = \frac{1}{3} \Rightarrow a = \frac{1}{\sqrt{3}} [∵ a > 0] \end{aligned}$

Area Question 25

Question 25

Engineering Preparation

Medical Preparation

NCERT Books & Solutions

Important Resources

Other Resources

Syllabus

Test Platform

Sample Mock Test

Mentorship

NCERT Exercise Video Solution

Area Question 25

Question 25

Engineering Preparation

Medical Preparation

NCERT Books & Solutions

Important Resources

Other Resources

Syllabus

Test Platform

Sample Mock Test

Mentorship

NCERT Exercise Video Solution

Menu