Area Question 19
Question 19
- The area enclosed by the curves $y=\sin x+\cos x$ and $y=|\cos x-\sin x|$ over the interval $0, \frac{\pi}{2}$ is (2014 Adv.) (a) $4(\sqrt{2}-1)$ (c) $2(\sqrt{2}+1)$ (b) $2 \sqrt{2}(\sqrt{2}-1)$ (d) $2 \sqrt{2}(\sqrt{2}+1)$
Show Answer
Solution:
- PLAN To find the bounded area between $y=f(x)$ and $y=g(x)$ between $x=$ a to $x=b$.
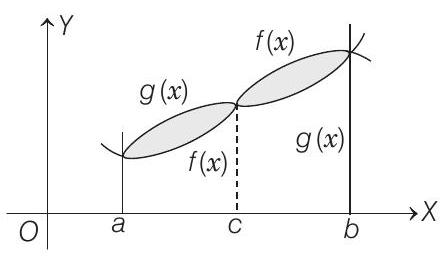
$\therefore \quad$ Area bounded $=\int_{a}^{\varepsilon}[g(x)-f(x)] d x+\int_{a}^{b}[f(x)-g(x)] d x$
$$ =\int_{a}^{b}|f(x)-g(x)| d x $$
Here,
$$ f(x)=y=\sin x+\cos x, \text { when } 0 \leq x \leq \frac{\pi}{2} $$
and
$$ g(x)=y=|\cos x-\sin x| $$
$$ =\begin{array}{ll} \cos x-\sin x, & 0 \leq x \leq \frac{\pi}{4} \ \sin x-\cos x, & \frac{\pi}{4} \leq x \leq \frac{\pi}{2} \end{array} $$
could be shown as
$\therefore$ Area bounded $=\int_{0}^{\pi / 4}{(\sin x+\cos x)-(\cos x-\sin x)} d x$ $+\int_{\pi / 4}^{\pi / 2}{(\sin x+\cos x)-(\sin x-\cos x)} d x$ $=\int_{0}^{\pi / 4} 2 \sin x d x+\int_{\pi / 4}^{\pi / 2} 2 \cos x d x$
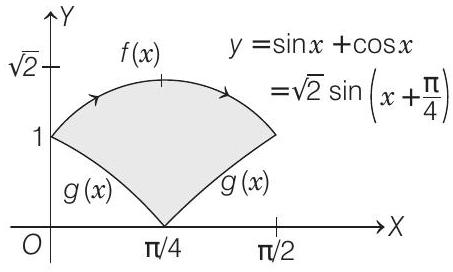
$=-2[\cos x]{0}^{\pi / 4}+2[\sin x \cdot n]{\pi / 4}^{\pi / 2}$ $=4-2 \sqrt{2}=2 \sqrt{2}(\sqrt{2}-1)$ sq units
