Area Question 17
Question 17
- The area (in sq units) of region described by
(2015 JEE Main)
(a)
Show Answer
Solution:
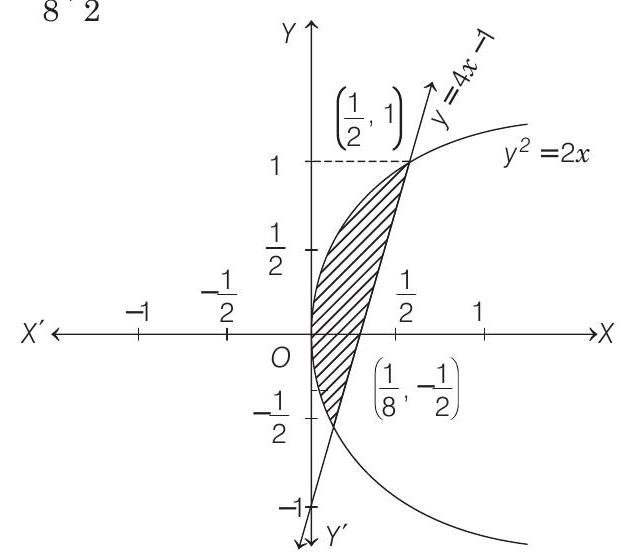
- Given region is
and
The point of intersection of the curves (i) and (ii) is
So, the points where these curves intersect are
$$ \begin{aligned} & =\frac{1}{4} \frac{y^{2}}{2}+y{ }{-1 / 2}^{-1}-\frac{1}{6}\left(y^{3}\right){-1 / 2}^{1} \ & =\frac{1}{4} \frac{1}{2}+1-\frac{1}{8}-\frac{1}{2}-\frac{1}{6} 1+\frac{1}{8} \ & =\frac{1}{4} \frac{3}{2}+\frac{3}{8}-\frac{1}{6} \frac{9}{8} \ & =\frac{1}{4} \times \frac{15}{8}-\frac{3}{16}=\frac{9}{32} \text { sq units } \end{aligned} $$






