Area Question 10
Question 10
- The area (in sq units) in the first quadrant bounded by the parabola, $y=x^{2}+1$, the tangent to it at the point $(2,5)$ and the coordinate axes is (2019 Main, 11 Jan II) (a) $\frac{14}{3}$ (b) $\frac{187}{24}$ (c) $\frac{8}{3}$ (d) $\frac{37}{24}$
Show Answer
Solution:
- Given, equation of parabola is $y=x^{2}+1$, which can be written as $x^{2}=(y-1)$. Clearly, vertex of parabola is $(0,1)$ and it will open upward.
Now, equation of tangent at $(2,5)$ is $\frac{y+5}{2}=2 x+1$
$\left[\because\right.$ Equation of the tangent at $\left(x_{1}, y_{1}\right)$ is given by $T=0$. Here, $\left.\frac{1}{2}\left(y+y_{1}\right)=x x_{1}+1\right]$ $y=4 x-3$
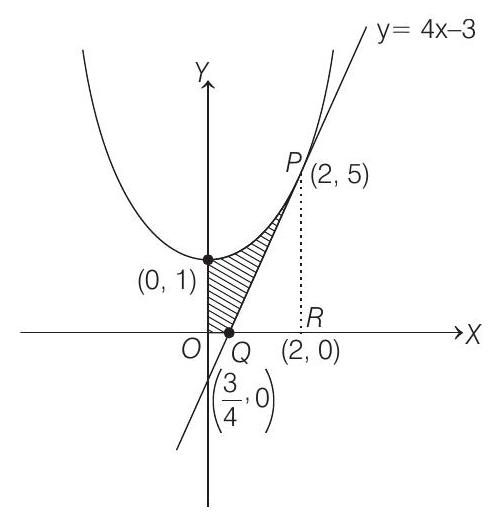
Required area $=$ Area of shaded region
$$ \begin{aligned} & =\int_{0}^{2} y(\text { parabola }) d x-(\text { Area of } \triangle P Q R) \ & =\int_{0}^{2}\left(x^{2}+1\right) d x-(\text { Area of } \triangle P Q R) \ & =\frac{x^{3}}{3}+x \quad-\frac{1}{2} 2-\frac{3}{4} \cdot 5 \end{aligned} $$
$\left[\because\right.$ Area of a triangle $=\frac{1}{2} \times$ base $\times$ height $]$
$$ \begin{aligned} & =\frac{8}{3}+2-0-\frac{1}{2} \frac{5}{4} 5 \ & =\frac{14}{3}-\frac{25}{8}=\frac{112-75}{24}=\frac{37}{24} \end{aligned} $$
