Application of Derivatives 4 Question 9
####10. Let $A(4,-4)$ and $B(9,6)$ be points on the parabola, $y^{2}=4 x$. Let $C$ be chosen on the arc $A O B$ of the parabola, where $O$ is the origin, such that the area of $\triangle A C B$ is maximum. Then, the area (in sq. units) of $\triangle A C B$, is
(2019 Main, 9 Jan II)
(a) $31 \frac{1}{4}$
(b) 32
(c) $31 \frac{3}{4}$
(d) $30 \frac{1}{2}$
Show Answer
Answer:
Correct Answer: 10. (a)
Solution:
- According to given information, we have the following figure.
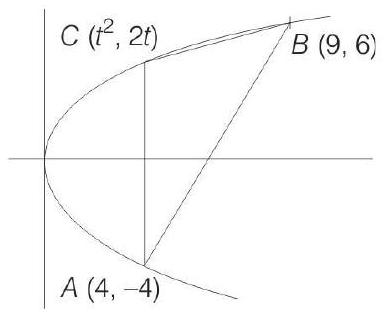
For $y^{2}=4 a x$, parametric coordinates of a point is $\left(a t^{2}\right.$, $2 a t)$.
$\therefore$ For $y^{2}=4 x$, let coordinates of $C$ be $\left(t^{2}, 2 t\right)$.
Then, area of $\triangle A B C=\frac{1}{2}|| \begin{array}{ccc}t^{2} & 2 t & 1 \\ 9 & 6 & 1 \\ 4 & -4 & 1\end{array} \mid$
$=\frac{1}{2}\left|t^{2}(6-(-4))-2 t(9-4)+1(-36-24)\right|$
$=\frac{1}{2}\left|10 t^{2}-10 t-60\right|=\frac{10}{2}\left|t^{2}-t-6\right|=5\left|t^{2}-t-6\right|$
Let, $\quad A(t)=5\left|t^{2}-t-6\right|$
Clearly, $A(4,-4) \equiv A\left(t_{1}^{2}, 2 t_{1}\right) \Rightarrow 2 t_{1}=-4$
$\Rightarrow \quad t_{1}=-2$
and $B(9,6) \equiv B\left(t_{2}^{2}, 2 t_{2}\right) \Rightarrow 2 t_{2}=6 \Rightarrow t_{2}=3$
Since, $C$ is on the arc $A O B$, the parameter ’ $t$ ’ for point $C \in(-2,3)$.
Let $f(t)=t^{2}-t-6 \Rightarrow f^{\prime}(t)=2 t-1$
Now, $\quad f^{\prime}(t)=0 \Rightarrow t=\frac{1}{2}$
Thus, for $A(t)$, critical point is at $t=\frac{1}{2}$
Now, $A \frac{1}{2}=5\left|\frac{1}{2}^{2}-\frac{1}{2}-6\right|=\frac{125}{4}=31 \frac{1}{4}$ [Using Eq. (i)]
