Application of Derivatives 4 Question 61
####64. Let $f: R \rightarrow R$ be defined as $f(x)=|x|+\left|x^{2}-1\right|$. The total number of points at which $f$ attains either a local maximum or a local minimum is
(2012)
Show Answer
Solution:
- PLAN
(i) Local maximum and local minimum are those points at which $f^{\prime}(x)=0$, when defined for all real numbers
(ii) Local maximum and local minimum for piecewise functions are also been checked at sharp edges.
Description of Situation $y=|x|=\begin{aligned} & x, \text { if } x \geq 0 \\ & -x, \text { if } x<0\end{aligned}$
Also, $\quad y=\left|x^{2}-1\right|=\begin{array}{ll}\left(x^{2}-1\right), & \text { if } x \leq-1 \text { or } x \geq 1 \\ \left(1-x^{2}\right), & \text { if }-1 \leq x \leq 1\end{array}$
$ y=|x|+\left|x^{2}-1\right|=\begin{array}{ll} -x+1-x^{2}, & \text { if } x \leq-1 \\ -x+1-x^{2}, & \text { if }-1 \leq x \leq 0 \\ x+1-x^{2}, & \text { if } 0 \leq x \leq 1 \\ x+x^{2}-1, & \text { if } x \geq 1 \\ -x^{2}-x+1, & \text { if } x \leq-1 \\ -x^{2}-x+1, & \text { if }-1 \leq x \leq 0 \\ -x^{2}+x+1, & \text { if } 0 \leq x \leq 1 \\ x^{2}+x-1, & \text { if } \quad x \geq 1 \end{array} $
which could be graphically shown as
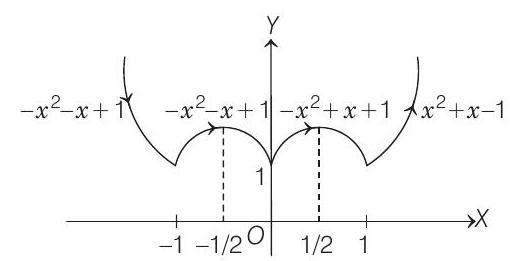
Thus, $f(x)$ attains maximum at $x=\frac{1}{2}, \frac{-1}{2}$ and $f(x)$ attains minimum at $x=-1,0,1$.
$\Rightarrow$ Total number of points $=5$
