Application of Derivatives 4 Question 60
####63. A vertical line passing through the point
If
Show Answer
Solution:
- PLAN As to maximise or minimise area of triangle, we should find area in terms of parametric coordinates and use second derivative test.
Here, tangent at
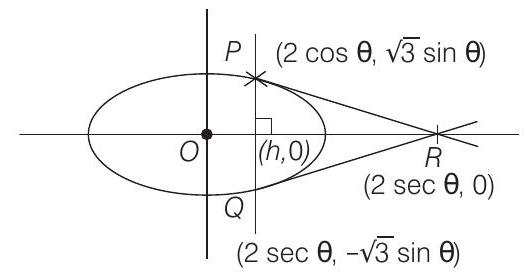
When
When
When






