Application of Derivatives 4 Question 6
####7. The shortest distance between the line $y=x$ and the curve $y^{2}=x-2$ is
(a) 2
(b) $\frac{7}{8}$
(c) $\frac{7}{4 \sqrt{2}}$
(d) $\frac{11}{4 \sqrt{2}}$
Show Answer
Answer:
Correct Answer: 7. (c)
Solution:
- Given equation of curve is
$ y^{2}=x-2 $
and the equation of line is
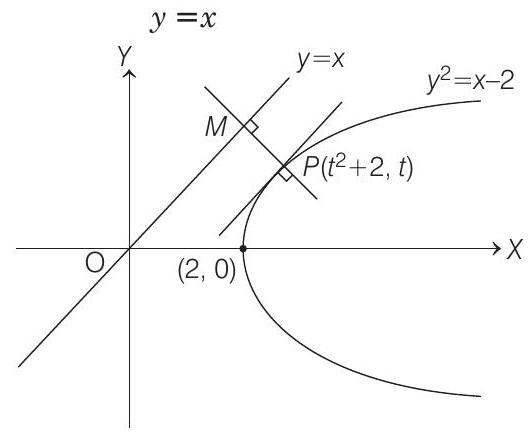
Consider a point $P\left(t^{2}+2, t\right)$ on parabola (i).
For the shortest distance between curve (i) and line (ii), the line $P M$ should be perpendicular to line (ii) and parabola (i), i.e. tangent at $P$ should be parallel to $y=x$. $\left.\therefore \frac{d y}{d x}\right|_{\text {at point } P}=$ Slope of tangent at point $P$ to curve (i) $=1 \quad[\because$ tangent is paralle $]$
$\left.\Rightarrow \quad \frac{1}{2 y}\right|_{P}=1$
to line $y=x]$
[differentiating the curve (i), we get $2 y \frac{d y}{d x}=1$ ]
$\Rightarrow \frac{1}{2 t}=1 \Rightarrow t=\frac{1}{2} \quad\left[\because P(x, y)=P\left(t^{2}+2, t\right)\right]$
So, the point $P$ is $\frac{9}{4}, \frac{1}{2}$.
Now, minimum distance $=P M=\frac{\frac{9}{4}-\frac{1}{2}}{\sqrt{2}}$
$\left[\because\right.$ distance of a point $P\left(x_{1}, y_{1}\right)$ from a line
$ \begin{gathered} a x+b y+c=0 \text { is } \frac{\left|a x_{1}+b y_{1}+c\right|}{\sqrt{a^{2}+b^{2}}} \\ =\frac{7}{4 \sqrt{2}} \text { units } \end{gathered} $
