Application of Derivatives 4 Question 59
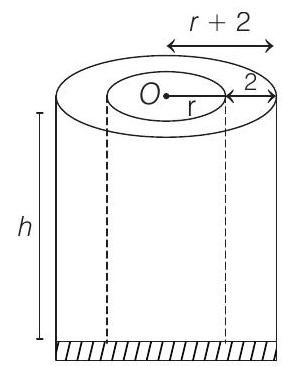
####62. A cylindrical container is to be made from certain solid material with the following constraints : It has a fixed inner volume of $V \mathrm{~mm}^{3}$, has a $2 \mathrm{~mm}$ thick solid wall and is open at the top. The bottom of the container is a solid circular disc of thickness $2 \mathrm{~mm}$ and is of radius equal to the outer radius of the container.
If the volume of the material used to make the container is minimum, when the inner radius of the container is $10 \mathrm{~mm}$, then the value of $\frac{V}{250 \pi}$ is
(2015 Adv.)
Show Answer
Solution:
- Here, volume of cylindrical container, $V=\pi r^{2} h$
and let volume of the material used be $T$.
$ \begin{aligned} & \therefore T=\pi\left[(r+2)^{2}-r^{2}\right] h+\pi(r+2)^{2} \times 2 \\ & \Rightarrow \quad T=\pi\left[(r+2)^{2}-r^{2}\right] \cdot \frac{V}{\pi r^{2}}+2 \pi(r+2)^{2} \\ & {\left[\because V=\pi r^{2} h \Rightarrow h=\frac{V}{\pi r^{2}}\right] } \end{aligned} $
$ \Rightarrow \quad T=V \frac{r+2}{r}{ }^{2}+2 \pi(r+2)^{2}-V $
On differentiating w.r.t. $r$, we get
$ \begin{aligned} & \qquad \frac{d T}{d r}=2 V \cdot \frac{r+2}{r} \cdot \frac{-2}{r^{2}}+4 \pi(r+2) \\ & \text { At } r=10, \frac{d T}{d r}=0 \end{aligned} $
Now,
$ 0=(r+2) \cdot 4 \pi-\frac{V}{r^{3}} $
where $\quad r=10$
$ \begin{aligned} & \Rightarrow \quad \frac{V}{1000}=\pi \\ & \text { or } \quad \frac{V}{250 \pi}=4 \end{aligned} $
