Application of Derivatives 4 Question 48
####50. The circle $x^{2}+y^{2}=1$ cuts the $X$-axis at $P$ and $Q$. Another circle with centre at $Q$ and variable radius intersects the first circle at $R$ above the $X$-axis and the line segment $P Q$ at $S$. Find the maximum area of the $\triangle Q S R$.
(1994, 5M)
Show Answer
Answer:
Correct Answer: 50. $(0,2)$
Solution:
- Since $x^{2}+y^{2}=1$ a circle $S_{1}$ has centre $(0,0)$ and cuts $X$-axis at $P(-1,0)$ and $Q(1,0)$. Now, suppose the circle $S_{2}$, with centre at $Q(1,0)$ has radius $r$. Since, the circle has to meet the first circle, $0<r<2$.
Again, equation of the circle with centre at $Q(1,0)$ and radius $r$ is
$ (x-1)^{2}+y^{2}=r^{2} $
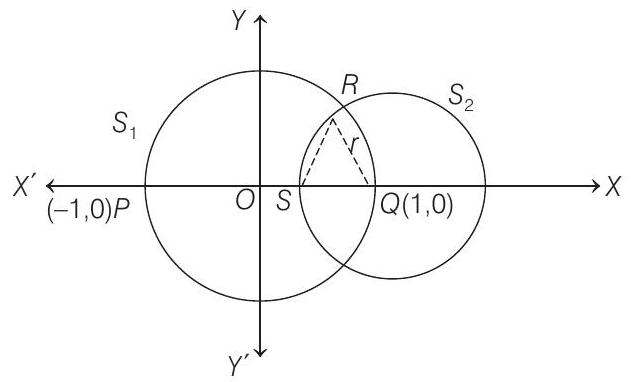
To find the coordinates of point $R$, we have to solve it with
$ x^{2}+y^{2}=1 $
On subtracting Eq. (ii) from Eq. (i), we get
$ \begin{aligned} & & (x-1)^{2}-x^{2} & =r^{2}-1 \\ & \Rightarrow & x^{2}+1-2 x-x^{2} & =r^{2}-1 \\ & \Rightarrow & 1-2 x & =r^{2}-1 \\ & \therefore & x & =\frac{2-r^{2}}{2} \end{aligned} $
On putting the value of $x$ in Eq. (i), we get
$ \begin{aligned} & \frac{2-r^{2}}{2}+y^{2}=1 \end{aligned} $
$ \begin{aligned} & =1-\frac{r^{4}-4 r^{2}+4}{4} \\ & =\frac{4-r^{4}+4 r^{2}-4}{4} \\ & =\frac{4 r^{2}-r^{4}}{4} \\ & =\frac{r^{2}\left(4-r^{2}\right)}{4} \\ & \Rightarrow \quad y=\frac{r \sqrt{4-r^{2}}}{2} \end{aligned} $
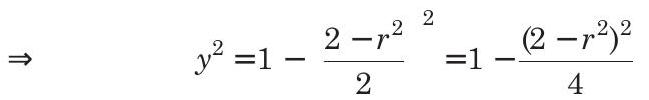
Again, we know that, coordinates of $S$ are $(1-r, 0)$, therefore
$ S Q=1-(1-r)=r $
Let $A$ denotes the area of $\triangle Q S R$, then
$ \begin{array}{rlrl} & A & =\frac{1}{2} r r \frac{\sqrt{4-r^{2}}}{2} \\ & =\frac{1}{4} r^{2} \sqrt{4-r^{2}} \\ \Rightarrow & A^{2}=\frac{1}{16} r^{4}\left(4-r^{2}\right) \\ \text { Let } & f(r)=r^{4}\left(4-r^{2}\right)=4 r^{4}-r^{6} \\ \Rightarrow \quad & f^{\prime}(r)=16 r^{3}-6 r^{5}=2 r^{3}\left(8-3 r^{2}\right) \end{array} $
For maxima and minima, put $f^{\prime}(r)=0$
$ \begin{array}{rlrl} \Rightarrow & & 2 r^{3}\left(8-3 r^{2}\right) & =0 \\ \Rightarrow & r & =0,8-3 r^{2}=0 \\ \Rightarrow & r & =0,3 r^{2}=8 \\ \Rightarrow & r & =0, r^{2}=8 / 3 \\ & \Rightarrow & r=0, r & =\frac{2 \sqrt{2}}{\sqrt{3}} \end{array} $
$ [\because 0<r<2, \text { so } r=2 \sqrt{2} / \sqrt{3}] $
Again, $\quad f^{\prime \prime}(r)=48 r^{2}-30 r^{4}$
$ \begin{aligned} \Rightarrow f^{\prime \prime} \frac{2 \sqrt{2}}{\sqrt{3}} & =48 \frac{4 \times 2}{3}-30 \frac{4 \times 2}{3}{ }^{2} \\ & =16 \times 8-\frac{10 \times 64}{3}=128-\frac{640}{3}=-\frac{256}{2}<0 \end{aligned} $
Therefore, $f(r)$ is maximum when, $r=\frac{2 \sqrt{2}}{\sqrt{3}}$
Hence, maximum value of $A$
$ \begin{aligned} & =\frac{1}{4} \frac{2 \sqrt{2}}{\sqrt{3}}_{2}^{4-\frac{2 \sqrt{2}}{\sqrt{3}}^{2}}=\frac{1}{4} \frac{8}{3} \cdot \sqrt{4-\frac{8}{3}} \\ & =\frac{2}{3} \cdot \frac{\sqrt{12-8}}{\sqrt{3}}=\frac{2 \cdot 2}{3 \sqrt{3}}=\frac{4}{3 \sqrt{3}}=\frac{4 \sqrt{3}}{9} \end{aligned} $
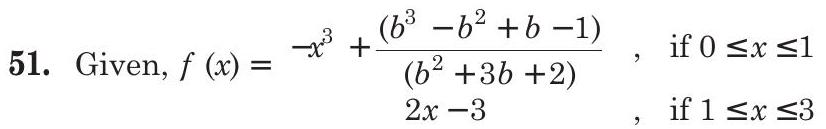is smallest at $x=1$.
So, $f(x)$ is decreasing on $[0,1]$ and increasing on $[1,3]$. Here, $f(1)=-1$ is the smallest value at $x=1$.
$\therefore$ Its smallest value occur as
$ \lim _{x \rightarrow 1^{-}} f(x)=\lim _{x \rightarrow 1^{-}}\left(-x^{3}\right)+\frac{\left(b^{3}-b^{2}+b-1\right)}{b^{2}+3 b+2} $
In order this value is not less than -1 , we must have
$ \begin{aligned} & \frac{b^{3}-b^{2}+b-1}{b^{2}+3 b+2} \geq 0 \\ & \Rightarrow \quad \frac{\left(b^{2}+1\right)(b-1)}{(b+1)(b+2)} \geq 0 \end{aligned} $
