####49. Let be a fixed point, where . A straight line passing through this point cuts the positive directions of the coordinate axes at the points and . Find the minimum area of the being the origin.
(1995, 5M)
Show Answer
Answer:
Correct Answer: 49. sq. units
Solution:
- Let equation of any line through the point is
For this line to intersect the positive direction of two axes, , since the angle in anti-clockwise direction from -axis becomes obtuse.
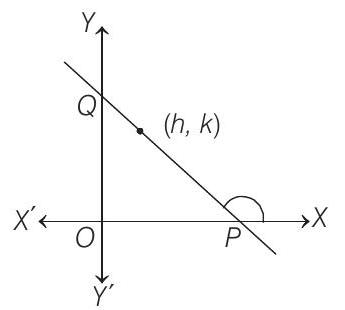
The line (i) meets -axis at and -axis at .
Let area of
To obtain minimum value of
[given]
Therefore, (only possible value).
Now,
Therefore, is least when . Also, the least value of is







