Application of Derivatives 4 Question 35
####37. If
(1993, 3M)
(a)
(b)
(c)
(d)
Match the Columns
Show Answer
Answer:
Correct Answer: 37. (a)
Solution:
- For
Hence,
Again, function is an algebraic polynomial, therefore it is continuous at
For continuity at
and
and
Therefore,
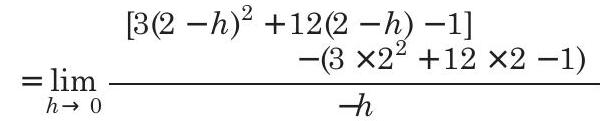
Since,
Again,






